A Performance-Based Comparison of C/C++ Compilers

Posted on November 11, 2017 in Benchmarks, Development Tools, Publications, Recent

This paper reports a performance-based comparison of six state-of-the-art C/C++ compilers: AOCC, Clang, G++, Intel C++ compiler, PGC++, and Zapcc. We measure two aspects of the compilers’ performance:

The speed of compiled C/C++ code parallelized with OpenMP 4.x directives for multi-threading and vectorization.
The compilation time for large projects with heavy C++ templating.

In addition to measuring the performance, we interpret the results by examining the assembly instructions produced by each compiler.

The tests are performed on an Intel Xeon Platinum processor featuring the Skylake architecture with AVX-512 vector instructions.

Colfax_Compiler_Comparison.pdf (562 KB)

1. The Importance of a Good Compiler
2. Testing Methodology
2.1. Meet the Compilers
2.2. Target Architecture
2.3. Computational Kernels
2.4. Compilation Time
2.5. Test Details
2.6. Test Platform
2.7. Code Analysis
3. Results
3.1. Performance of Compiled Code
3.2. Compilation Speed
4. Summary
Appendix A. LU Decomposition
Appendix B. Jacobi Solver
Appendix C. Structure Function
Appendix D. Compilation Speed

1. The Importance of a Good Compiler

Modern x86-64 CPUs are highly complex CISC architecture machines. Modern vector extensions to the x86-64 architecture, such as AVX2 and AVX-512, have instructions developed to handle common computational kernels. For example, the fused multiply-add instruction is used to increase the performance and accuracy in dense linear algebra, collision detection instruction is suitable for the operation of binning in statistical calculations, and bit-masked instructions are designed for handling branches in vector calculations. However, workloads with complex memory access patterns and non-standard kernels require considerable work from both the programmer and the compiler in order to achieve the highest performance.

At the same time, modern language standards work hard to abstract away the details of the underlying hardware and data structures and generate generic code that aligns more with logic and mathematics than instructions and memory locations. Newer language standards place greater emphasis on constructs that allow programmers the ability to express their intent. Modern standards of the C++ language are moving in the direction of greater expressivity and abstraction. The Python programming language is popular because of its readability and expressiveness, even at the cost of reduced runtime speed. Human-readable, expressive languages enable bug-free, maintainable code and are here to stay.

The consequence of increasing expressivity is an increased burden on the compiler to produce good assembly code from the complex high-level constructs written by the programmers. Compilers have to be smarter and work harder to wring the most performance out of code. Not all compilers are created equal and some are better than others at taking the same piece of code and producing efficient assembly.

In addition to producing fast executables, modern compilers must be fast themselves. Large software projects in C/C++ can span hundreds to thousands of individual translation units, each of which can be hundreds of lines in length. C++ code can also make heavy use of techniques such as template programming that require multiple passes from the compiler to produce object files. The compile time for large C++ projects can run into hours. Developers use practices like precompiled header files to reduce the compilation time. Large projects usually feature teams of developers with multiple interdependent changes being committed simultaneously. Each commit may require upstream developers to recompile significant portions of the codebase. Faster compilers are crucial to achieving high productivity from large teams.

Finally, there’s language extensions. Leveraging a modern computing system with multiple cores, vector processing capabilities, and accelerators goes beyond the natural capabilities of common programming languages. So frameworks specific to high-performance computing (HPC), such as OpenMP and OpenACC, step in to fill this gap. These frameworks offer APIs with which programmers can express parallelism in the code. The compiler, along with the corresponding runtime libraries, must map this parallel code onto the processor architecture. Numerous HPC projects rely on the OpenMP and OpenACC standards, and the standards are being expanded by the developers and hardware manufacturers. Therefore, compilers must constantly play catch up with the evolving standards for language extensions.

What is a good compiler? A good compiler should let us focus on the process of writing programs rather than struggling with the inadequacies of the compiler. It should compile the most recent language standards without complaint. We should feel confident in its ability to produce well-optimized code from even the most abstract codebase. Lastly, it should compile source code as quickly as possible.

2. Testing Methodology

2.1. Meet the Compilers

We aim to test the most commonly available C/C++ compilers. To be considered as a candidate for our test, the compiler must

be listed on the Wikipedia list of C/C++ compilers,
compile for the x86-64 architecture,
be available for Linux platforms,
be under active development.

The following six compilers pass our criteria:

Intel C++ Compiler 18.0.0 (Intel C++ compiler)
GNU Compiler Collection 7.2.0 (G++)
PGI® C++ Compiler 17.4 (PGC++)
Clang 5.0.0 (Clang)
Zapcc Compiler 1.0.1 (Zapcc)
AMD Optimizing C/C++ Compiler 1.0 (AOCC)

The Intel C++ compiler compiler is made by the Intel Corporation and is highly tuned for Intel processors. Intel C++ compiler features support for the latest C++ and OpenMP standards, as well as support for the latest Intel architectures. Intel C++ compiler is available free of charge for student and open source developers. For OpenMP support, by default it links against the Intel libiomp5.so library.

The G++ compiler is an open-source compiler made by the Free Software Foundation Inc. G++ was originally written to be the compiler for the GNU operating system. It is capable of generating code for a large number of target architectures and is widely available on Unix-like platforms. For OpenMP support, we link against the GNU libgomp.so library.

The following three compilers are based on the LLVM infrastructure for code generation.

The Clang compiler is developed by the LLVM project. The project aims to produce a fully G++Collection-compliant compiler suite that can replace the G++Collection. We use LLVM 5.0.0, the most recent release of the LLVM infrastructure. For better performance, we instruct Clang to use the Polly loop optimizer and the native lld linker. We link against the LLVM provided OpenMP library libomp.so.

Zapcc made by Ceemple Software Ltd. is a replacement for Clang that aims to compile code much faster than Clang. Zapcc uses the LLVM 5.0.0 backend for optimization, code generation, and also for libraries such as libomp.so.

AOCC is an AMD-tweaked version of the Clang 4.0.0 compiler optimized for the AMD Family 17h processors (‘Zen’ core). AMD enhancements include improved vectorization, high-level optimizer, whole program optimization, & code generation. The AMD compiler ships with its own versions of the LLVM libraries. For OpenMP support we link against the AMD provided libomp.so.

PGC++ is made by the Portland Group and features extensive support for the latest OpenACC 2.5 standard. PGC++ is available both as a free Community Edition (PGC++ 17.4) as well as a paid Professional Edition (PGC++ 17.9). At the time of writing, an LLVM-based beta edition with support for enables OpenMP 4.5 extensions is available for testing. The Portland Group is working to incorporate AVX-512 code generation abilities into PGC++. We show results obtained with the free Community Edition (PGC++ 17.4). PGC++ comes with its own set of libraries. For OpenMP support, we link against the PGI OpenMP library libpgmp.so

2.2. Target Architecture

The Intel Xeon Scalable processor family released in 2017 is based on the Skylake (SKL) microarchitecture, which succeeds the Broadwell (BDW) microarchitecture. The SKL microarchitecture introduces AVX-512 instructions, which feature twice the vector width and number of available vector registers as compared to AVX2 instructions available in the BDW microarchitecture. Properly written algorithms are capable of yielding 2x the performance on a SKL machine as compared to a BDW machine with a similar clock speed and core count.

All the tested compilers issue AVX-512 instructions except PGC++. AVX-512 support is under development for PGC++. Due to the lack of AVX-512 support, PGC++ performs substantially worse in some of the benchmarks than the other compilers.

2.3. Computational Kernels

To test the performance of compiled HPC code, we offer to the compilers three computational microkernels:

A straightforward implementation of the pivotless LU decomposition with simple data structures and memory access pattern, and without any hand-tuning. Although this kernel can be optimized to the point at which it is compute bound, we test the un-optimized version of the kernel in order to determine how each compiler handles ‘naive’ source code with complex vectorization and threading patterns hidden within.
A highly abstracted object-oriented implementation of a Jacobi solver for the Poisson problem on a square domain. This kernel tests how well the compilers can perform complex, cross-procedural code analysis to detect common parallel patterns (in this case, a 5-point stencil). This is a bandwidth-bound kernel, meaning that its performance is limited by the RAM bandwidth rather than by the floating-point arithmetic capabilities of the cores.
A heavily-tuned implementation of structure function computation. We fully optimize this kernel to the point where it is compute-bound, i.e., limited by the arithmetic performance capabilities of the CPU. The purpose of this test is to see how efficient the resulting binary is when the source code is acutely aware of the underlying architecture.

We use OpenMP compiler extensions for vectorizing and parallelizing our computational kernels. OpenMP 3.1 extensions are supported by all 6 compilers. OpenMP 4.x introduces constructs for SIMD programming, including reduction and alignment clauses. OpenMP 4.x is supported by all the compilers with varying degrees of compliance with the exception of PGC++. Full OpenMP 4.5 support is forthcoming in a future LLVM-based version of PGC++. To level the playing field in anticipation of OpenMP 4.5 support by PGC++, we use the PGI-specific directive #pragma loop ivdep to inform PGC++ that loop iterations are independent for the following loop and can be safely executed simultaneously. This allows PGC++ to issue vector instructions for the following loop and has the same effect as the OpenMP 4.x directive #pragma omp simd for the other compilers.

2.4. Compilation Time

Our compile problem consists of compiling the TMV linear algebra library written by Dr. Mike Jarvis of the University of Pennsylvania. TMV stands for ‘templated matrix vector’. As the name suggests, this library contains templated linear algebra routines for use with various special matrix types. This makes TMV representative of scenarios where compilation speed is a significant factor in developer productivity.

2.5. Test Details

We provide the code used in this comparison in a GitHub repository at https://github.com/ColfaxResearch/CompilerComparisonCode. Each computational kernel is implemented in C++. The performance-critical function is located in the file ‘critical.cpp‘. The main function manages memory and calls the critical function to execute the computational kernel. We solve each problem NUM_PROBLEMS number of times to obtain the performance figure for a single ‘trial’. Each trial is repeated NUM_TRIALS number of times and the results of the first 3 trials discarded. The remaining trials are averaged to get the final performance figure for the run. Finally, we run each test NUM_RUNS number of times and select the most favorable result. This process ensures that we get consistent, reproducible results.

For multi-threaded performance, we empirically determine the optimal number of threads for each combination of the compiler, kernel, and problem size. I.e., we do not assume that the same thread count is optimal for code generated by all the compilers.

2.6. Test Platform

Our test platform is a 2-socket Intel Xeon Platinum 8168 machine (Skylake microarchitecture) with 48 physical cores at 2.7 GHz and 192 GB of RAM.

The theoretical peak performance of a system can be computed using

P = f × n_cores × v × i_cyc × F_instruc, (1)

where P is the performance in GFLOP/s, f is the clock frequency in GHz, n_cores is the number of available cores, v is the vector width, i_cyc is the number of instructions that can be executed per clock cycle, and F_instruc is the number of floating point operations performed per instruction.

As per the Intel Xeon Scalable family specifications, the maximum clock frequency of Platinum 8168 CPU is 2.5 GHz when executing AVX-512 instructions on 24 cores per socket. For double precision FMA, v=8 and F_instruc=2. Each Platinum 8168 CPU socket has 24 cores for a total of 48 cores on a 2-socket system. Each core has two FMA units, making i_cyc = 2. Therefore, the theoretical peak performance of our system for purely FMA double precision computations is

P_×48^FMA = 2.5 × 48 × 8 × 2 × 2 = 3840 GFLOP/s.

Non-FMA computational instructions such as vaddpd, vmulpd, and vsubpd also execute on the Skylake FMA units. However, each instruction only performs a single computation making F_instruc=1. Therefore, the theoretical peak performance of our system for purely non-FMA double precision computations is

P_×48 = 2.5 × 48 × 8 × 2 × 1 = 1920 GFLOP/s.

When executing AVX-512 instructions with a single core, the maximum clock frequency of the Platinum 8168 CPU is 3.5 GHz. The corresponding theoretical peak performance is P_×1^FMA=112 GFLOP/s for purely FMA double precision computations and P_×1=56 GFLOP/s for purely non-FMA double precision computations.

2.7. Code Analysis

We find that the best way to determine the reasons for performance differences between codes produced by the different compilers is by looking at the assembly instructions generated by each compiler. We generate assembly from the compiled object file for each compiler using objdump. Our command line for generating the assembly is

objdump -d -S -l -M intel
    critical.o &> critical.asm

This combination of flags outputs assembly using the Intel syntax. We edit the output assembly to remove extraneous information and compiler comments.

3. Results

3.1. Performance of Compiled Code

In this section, we present and comment on the timing results. For an explanation of these values, please refer to the Appendices. There, we conduct a detailed analysis of the behavior of each computational kernel when compiled by the different compilers as well as a general overview of the kernels themselves. Compilation arguments and relevant snippets of code and assembly can also be found in the Appendices.

Table 1 summarizes our findings.

Compiler	LU Serial	LU Parallel	Threads	Jacobi Serial	Jacobi Parallel	Threads	SF Serial	SF Parallel	Threads	TMV Compile
PGC++	11.0	103	24	4.28	30.7	13	12.8	n/a	n/a	2750
Clang	8.22	75.3	15	4.39	42.3	20	23.3	837	96	902
AOCC	9.57	96.4	15	4.72	58.2	44	57.2	1990	96	1230
Zapcc	8.21	74.7	15	4.40	41.4	21	23.4	841	96	510
G++	14.3	90.9	12	12.8	74.4	9	36.4	1380	96	848
IntelC++	14.6	118	15	15.0	103	14	57.4	2050	48	1420

Table 1: Results of compiler comparison. Values in columns LUDecomp, JacobiSolve and SFComp are in GFLOP/s (more is better), and in column TMV the value is in seconds (less is better)

Figure 1 plots the relative performance of the computational kernels when compiled by the different compilers and run with a single thread. The performance values are normalizes so that the performance of G++ is equal to 1.0. The normalization constant is different for different kernels.

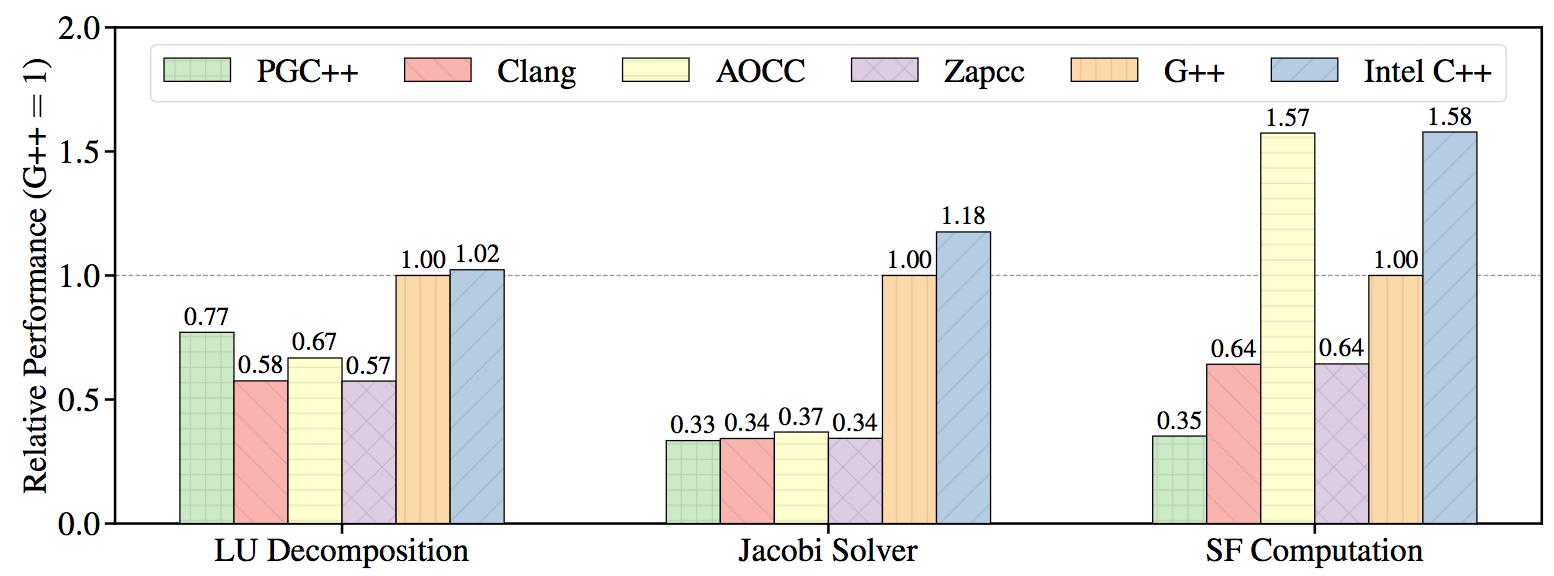
Figure 1: Relative performance of each kernel as compiled by the different compilers. (single-threaded, higher is better).

Noticably, the LLVM 5.0.0 based Clang & Zapcc provide almost identical performance across the board. This is to be expected because the two compilers are very similar with the only difference being that Zapcc has been tweaked to improve the compile speed of Clang.

The PGI compiler provides higher performance than LLVM-based compilers in the first text, where the code has vectorization patterns, but is not optimized. While both G++ & Intel C++ compiler provide even higher performance, the behavior should be seen in light of the fact that PGC++ is incapable of issuing AVX-512 for the time being and is therefore using only half the vector width of the other compilers in this test.

The GNU and Intel compilers stand out in the second, bandwidth-bound test, where the data parallelism of a stencil operator is obscured by the abstraction techniques of the C++ language. These two are the only compilers that manage to successfully vectorize the computational kernel used in this test. The other compilers issue scalar instructions and therefore provide low performance.

The AMD & Intel compilers stand out in the third, compute-bound test, where the code is highly tuned for the SKL architecture. Both compilers manage to minimize reading and writing to memory. The other compilers use larger numbers of memory reads and writes, leading to lower performance. The PGI compiler, due to its current limitations, is issuing AVX2 instructions with half the vector width of the AVX-512 instructions issued by the other compilers.

Figure 2 shows the performance results with multi-threading. The plotted quantity is a relative performance measured with the optimal thread count for each compiler and kernel. Again, performance normalization is chosen so that the performance of G++ is equal to 1, and the normalization constant is specific to each kernel.

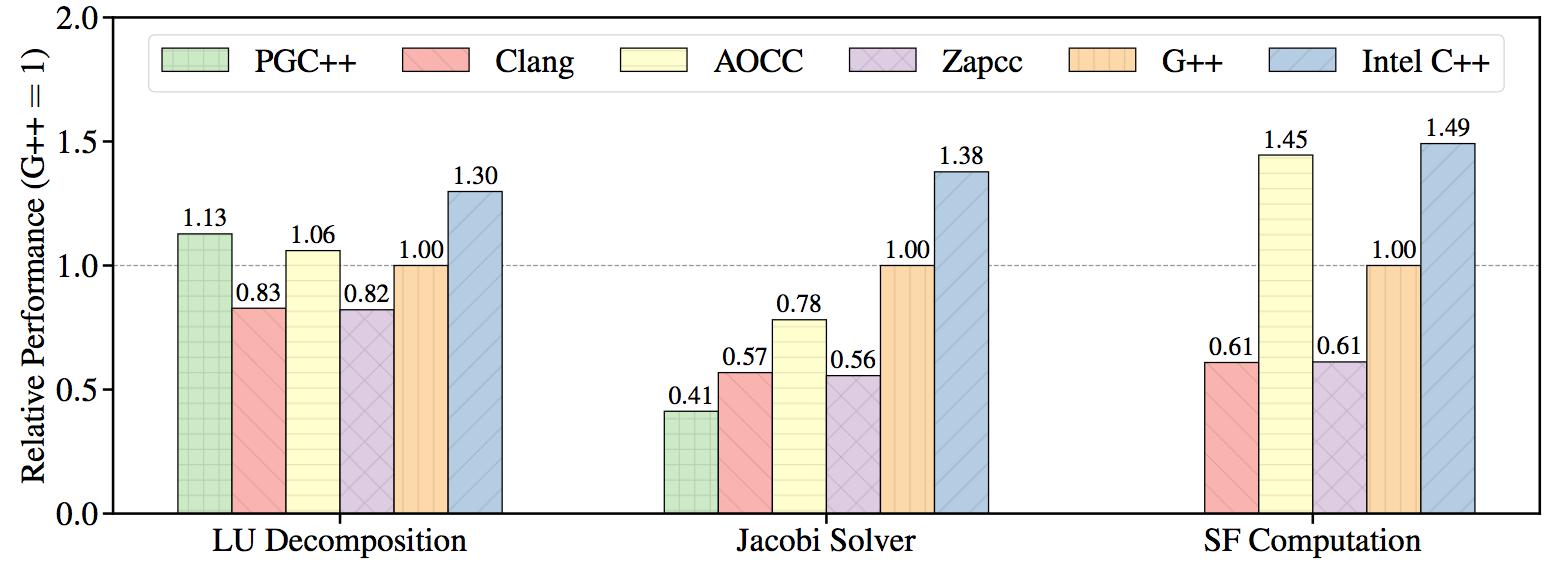
Figure 2: Relative performance of each kernel as compiled by the different compilers. (multi-threaded, higher is better).

The relative performance of the compilers does not change much when running the structure function workloads with multiple threads. However, in the case of the Jacobi solver and LU decomposition kernels, the AMD compiler shows larger improvements relative to the other compilers. We believe that this is due to the AMD optimized OpenMP implementation used by AOCC.

3.2. Compilation Speed

Figure 3 shows the relative compilation time of the TMV library when compiled by the different compilers. The plotted values are the reciprocals of the compilation time, normalized so that G++ performance is equal to 1.

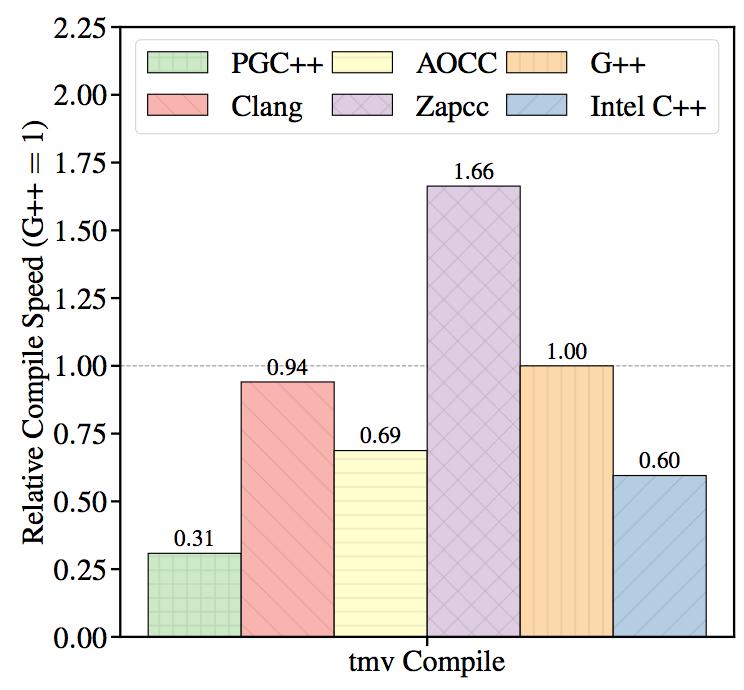
Figure 3: Compilation speed measured by compiling the TMV library. (multi-threaded, higher is better).

The Zapcc compiler is the fastest compiler in this test, handily beating the nearest competitor by a factor of more than 1.6x. The PGI compiler is the slowest compiler in the test. According to the Portland Group website, they are working on an LLVM-based update to the PGI compiler, which may improve the compile time.

4. Summary

Different compilers produce executables with differing levels of performance even when given the same OpenMP standard-based source code to compile. The compile speed can also vary from compiler to compiler. We see a difference of

1.8x in performance between the best (Intel compiler) and worst compiler (Zapcc compiler) on our LU decomposition kernel (non-optimized, complex vectorization pattern).
3.5x in performance between the best (Intel compiler) and worst compiler (PGI compiler) on our Jacobi solver kernel (bandwidth-limited stencil obscured by abstraction techniques).
2.5x in performance between the best (Intel compiler) and worst compiler (LLVM clang compiler) on our Structure Function kernel (highly-tuned code for SKL).
5.4x in compile time between the best (Zapcc compiler) and worst compiler (PGI compiler) on our TMV compilation test (large templated library).

In the case of the computational kernels, the performance difference can be attributed to how each compiler implements the same sequence of arithmetic instructions. Different implementations require differing numbers of registers, memory operations, etc. that make some implementations faster and others slower. We discuss these details in the Appendices.

Modern CPUs are highly pipelined, superscalar machines that execute instructions out-of-order, use speculative execution, prefetching, and other performance-enhancing techniques. This makes it difficult to predict exactly how well a sequence of instructions will execute on any given microarchitecture. Hardware engineers use highly sophisticated simulations to overcome these problems when designing new CPUs. Compilers have to use heuristics to decide how to target specific CPU microarchitectures and thus have to be tuned to produce good code. Furthermore, the tuning is workload-specific, i.e., a generally sub-par compiler may produce the best code for certain workloads, even though it generally produces poorer code on average.

The tests in this work and our own experience suggest that the Intel compiler generally produces good code for a wide range of problems. Our computational kernels suggest that the Intel C++ compiler is generally able to provide the best performance because it has a better picture of the target machine architecture, i.e., it knows how to exploit all available registers, minimize memory operations, etc. Intel C++ compiler also has good support for the newer C++ and OpenMP standards. In our tests, Intel C++ compiler compiles complex code approximately 40% slower than G++. The Intel compiler has detailed documentation, code samples, and is able to output helpful optimization reports (see, e.g., this paper) that can be used to determine how to further improve application performance. Lastly, the Intel compiler is a part of a suite of libraries and tools, such as Intel MKL, Intel Advisor, Intel VTune Performance Analyzer, etc., which are very helpful for high-performance application development.

The GNU compiler also does very well in our tests. G++ produces the second fastest code in three out of six cases and is amongst the fastest compilers in terms of compile time. From a standards compliance standpoint, G++ has almost complete support for the new C++11 standard. GNU documentation is generally good, although it can be somewhat difficult to find details about obscure features. GNU optimization reports are exceedingly verbose making it very tedious to determine simple issues, such as if a given loop vectorized. Lastly, G++ has the added advantage of being open-source and freely available.

The LLVM-based Clang and Zapcc compilers produce executables with average performance but feature amongst the fastest compilers in the suite. The Zapcc is the fastest compiler in our compile test. LLVM and Clang have relatively good documentation, although it can be somewhat unclear as to which version of the product the documentation refers to. The Zapcc compiler relies entirely on the standard LLVM documentation. As LLVM matures, we expect the performance from all the LLVM-based compilers to keep increasing.

AMD’s AOCC compiler manages to tie with the Intel compiler in the compute-bound test and puts in a good showing in the Jacobi solver test. This is impressive given that AOCC is relatively new and targets an entirely different microarchitecture. At the moment, this compiler does not have much documentation, instead relying on LLVM documentation. We hope that AMD continues to improve AOCC and add high performance libraries for scientific computing as AOCC matures.

While all the LLVM-based compilers generate optimization reports, the reports do not contain enough helpful information about why the compiler chose to make certain decisions. This makes it unduly difficult to determine the best course of action to take to improve performance.

The PGI compiler’s strongest suit is its support for latest OpenACC 2.5 standard, which primarily applies to GPGPU programming. At the same time, PGC++ is capable of generating good x86 code as seen in the LU decomposition test. It lags behind its peers when it comes to support for new ISA extensions (AVX-512) and the latest OpenMP standards. Support for these features is in the works. The PGI compiler has good documentation and emits helpful and clear optimization reports. Like the Intel compiler, PGC++ comes with a suite of performance monitoring and optimization tools that add value for the developer.

Appendix A. LU Decomposition

A.1. What is pivotless LU Decomposition and How does it work?

LU decomposition is a fundamental matrix decomposition method that finds application in a wide range of numerical problems when solving linear systems of equations. The goal of LU decomposition is to represent an arbitrary square, non-degenerate matrix A as the product of a lower triangular matrix L with an upper triangular matrix U. The usual LU decomposition algorithms feature pivoting to avoid numerical instabilities. Pivotless LU decomposition is used when the matrix is known to be diagonally dominant and for solving partial differential equations (PDEs) ? for example, for the computation of preconditioners, where numerical accuracy is a secondary requirement to speed.

We use the pivotless Dolittle algorithm to implement LU decomposition. The pivotless Dolittle algorithm chooses to make L unit-triangular. For an input n×n matrix A, the Dolittle method performs n-1 iterations to compute L & U. We use the notation A^(b) to denote the matrix A after the b-th iteration. On iteration b, the b-th row of A^(b-1) is multiplied by a factor and added to all the rows below it. The multiplication factor is chosen to make all the elements in column b starting from row b+1 equal to zero in A^(b). The multiplication factor is recorded as the i,j-th entry of L while A slowly transforms into U.

Start with

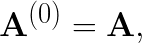$\mathbf{A}^{(0)} = \mathbf{A},$ (2)

For step b ranging from 0 to n-1, compute

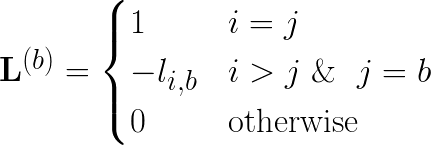$\mathbf{L}^{(b)} = \begin{cases} 1 & i = j \\ -l_{i,b} & i > j \text{\ \& \ } j = b \\ 0 & \text{otherwise} \end{cases}$ (3)

with

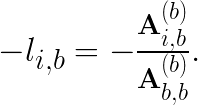$-l_{i,b} = -\frac{\mathbf{A}^{(b)}_{i,b}}{\mathbf{A}^{(b)}_{b,b}}.$ (4)

Use L^(b) to compute A^(b+1) using

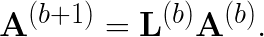$\mathbf{A}^{(b + 1)} = \mathbf{L}^{(b)}\mathbf{A}^{(b)}.$ (5)

After n-1 steps, U = A^(n-1) and L = L^(n-1).

The Dolittle algorithm can be implemented in-place because L is unit-triangular, i.e., all of its diagonal elements are equal to 1. As a consequence, there is no need to store the diagonal entries of L. Rather, A is overwritten as the iterations proceed, leaving the non-diagonal portions of L in the lower triangular section of A and U on the upper triangle.

Listing 1 shows our implementation of the pivotless Dolittle algorithm for LU decomposition.

  void LU_decomp_kij_opt(const int n, const int lda, double * A,
                         double * scratch) {

    for (int k = 0; k < n; ++k) {
      const double recAkk = 1.0/A[k*lda + k];
#pragma omp parallel for
      for (int i = k + 1; i < n; ++i) {
        A[i*lda + k] = A[i*lda + k]*recAkk;
#ifdef __PGI
#pragma loop ivdep
#else
#pragma omp simd
#endif
        for (int j = k + 1; j < n; ++j)
          A[i*lda + j] -= A[i*lda + k]*A[k*lda + j];
      }
    }
  }

Listing 1: LU Decomposition implementation.

This implementation of the Dolittle ordering is known as the KIJ-ordering due to the sequence in which the three for-loops are nested. The memory access pattern of the KIJ-ordering is optimal as compared to other possible orderings. The KIJ-ordering can be readily vectorized & parallelized across the J & I loops, respectively.

It is possible to further optimize the KIJ ordering by regularizing the vectorization pattern and tiling the loops to increase data reuse (e.g., this paper). We do not implement these optimizations in order to see how the compilers behave with unoptimized code.

LU decomposition requires (2/3)n³ operations, where n is the size of the matrix. We test with matrices of size n=256 when testing for single threaded performance. For multithreaded performance, we increase the problem size to n=1024.

We discuss the assembly code generated by each compiler to gain further insight.

A.2. Intel C++ compiler

We compile the code using the compile line in Listing 2.

icpc -o critical.o -c critical.cpp
     -D__ALGORITHM__=KIJ_OPT -D__AUTO__
     -O3 -std=c++14
     -qopenmp -qopenmp-simd
     -qopt-report=5
     -qopt-assume-safe-padding
     -xCORE-AVX512
     -qopt-zmm-usage=high

Listing 2: Compile line for compiling the LU Decomposition critical.cpp source file with Intel C++ compiler.

Listing 3 shows the assembly instructions generated by Intel C++ compiler for the inner J-loop using the Intel syntax. All the computation in the inner loop is performed by a single AVX-512F FMA instruction. The other instructions are AVX-512 memory access instructions along with a handful of scalar x86 instructions for managing the loop. 4 out of 32 zmm registers are used in the loop.

2f0: vmovups         zmm3,[rdi+rsi*8+0x8]
2fb: vbroadcastsd    zmm4,[rcx+r8*8]
302: vfnmadd213pd    zmm4,zmm3,[r11+rsi*8+0x8]
30d: vmovupd         [r11+rsi*8+0x8],zmm4
318: vmovups         zmm5,[rdi+rsi*8+0x48]
323: vbroadcastsd    zmm6,[rcx+r8*8]
32a: vfnmadd213pd    zmm6,zmm5,[r11+rsi*8+0x48]
335: vmovupd         [r11+rsi*8+0x48],zmm6
340: add             rsi,0x10
344: cmp             rsi,r13
347: jb              2f0

Listing 3: Assembly of critical J-loop produced by the Intel compiler.

On our test system (see Section 2.6), this sequence of instructions yields 14.62 GFLOP/s in single threaded mode and 118.06 GFLOP/s when running with 15 threads for a 8.1x speedup (0.54x/thread).

Intel C++ compiler unrolls the J-loop by a factor of 2x. Each instruction performs a memory access, including the two FMA instructions on lines 302 and 32a.

A possible inefficiency is the duplicated broadcast instruction on lines 2fb and 323. The registers used in the broadcast are also the destination registers in the following FMA operations making it impossible to simply drop one usage.

Interchanging the registers used in each FMA and subsequent store operation, i.e., swapping zmm3 with zmm4 in lines 302 and 30d and swapping zmm5 with zmm6 in lines 323 and 32a makes it possible to eliminate the use of either zmm4 or zmm6. It is also possible to hoist the remaining broadcast operation outside the loop. We speculate that these transformations can yield further performance improvements.

A.3. G++

We compile the code using the compile line in Listing 4.

g++ -o critical.o -c critical.cpp
    -D__ALGORITHM__=KIJ_OPT -D__AUTO__
    -O3 -std=c++14 -m64 -ffast-math
    -fassociative-math -ftree-vectorize
    -ftree-vectorizer-verbose=0
    -fopenmp -fopenmp-simd
    -fopt-info-all=luDecomp.o.gnurpt
    -march=skylake-avx512

Listing 4: Compile line for compiling the LU Decomposition critical.cpp source file with G++.

Listing 5. shows the assembly instructions generated by G++ for the time consuming inner col-loop using the Intel syntax. 2 out of the 32 available zmm registers are used in the loop.

2f0: vmovupd         zmm1,[r10+rax*1]
2f7: vfnmadd213pd    zmm1,zmm2,[rsi+rax*1]
2fe: add             edx,0x1
301: vmovapd         [rsi+rax*1],zmm1
308: add             rax,0x40
30c: cmp             edx,r11d
30f: jb              2f0

Listing 5: Assembly of critical j-loop produced by the GNU compiler.

On our test system, this sequence of instructions yields 14.29 GFLOP/s in single threaded mode and 90.94 GFLOP/s when running with 12 threads for a 6.4x speedup (0.53x/thread).

Unlike Intel C++ compiler, G++ does not unroll the loop. Each loop iteration performs a single pass of the loop-update operation. Even though the GNU compiler compiled code performs one less memory operation per loop-update, it runs slightly slower than the code generated by the Intel compiler. We speculate that this may be attributable to the overuse of scalar variables used to control the loop and index memory accesses.

A.4. PGC++

We compile the code using the compile line in Listing 6.

pgc++ -o critical.o -c critical.cpp
      -D__ALGORITHM__=KIJ_OPT -D__AUTO__
      -O3 -tp=haswell -fast -O4 -fma
      -Msmart -Mfma -Mcache_align
      -Mipa=all -Mmovnt -mp -Mquad
      -Msafeptr=all -Minfo=all
      -Mnoprefetch

Listing 6: Compile line for compiling the LU Decomposition critical.cpp source file with PGC++.

The PGI compiler generates three versions of the J-loop that use slight variations to optimally execute the loop body. All three variations unroll the loop by a factor of 2x. The first variation uses just 3 memory instructions per evaluation of the loop-body, retaining the value of A[i*lda + k] in the zmm0 register instead of broadcasting it on every loop iteration the way the Intel C++ compiler generated code does. The zmm0 register is re-used in the second unrolled loop iteration, minimizing the number of memory accesses made in the loop body. The second variation eliminates one register, preferring instead to perform the required memory read operation as a part of the FMA instruction. The third variation is very similar to the first variation but uses streaming stores to reduce pressure on the caches.

Listing 7 shows the assembly instructions generated by PGC++ for the three variations of the time consuming inner col-loop using the Intel syntax. 2 out of the 16 available ymm registers are used.

1a8: vmovupd         ymm1,[rsi+rcx*1]
1ad: vmovupd         ymm2,[rdx+rcx*1]
1b2: sub             eax,0x8
1b5: vfnmadd231pd    ymm2,ymm1,ymm0
1ba: vmovupd         [rdx+rcx*1],ymm2
1bf: vmovupd         ymm2,[rcx+rdx*1+0x20]
1c5: vmovupd         ymm1,[rcx+rsi*1+0x20]
1cb: vfnmadd231pd    ymm2,ymm1,ymm0
1d0: vmovupd         [rcx+rdx*1+0x20],ymm2
1d6: add             rcx,0x40
1da: test            eax,eax
1dc: jg              1a8

2e0: vmovupd         ymm1,[rsi+rdx*1]
2e5: add             ecx,0x8
2e8: sub             eax,0x8
2eb: vfnmadd231pd    ymm1,ymm0,[r8+rdx*1]
2f1: vmovupd         [rsi+rdx*1],ymm1
2f6: vmovupd         ymm2,[rdx+rsi*1+0x20]
2fc: vfnmadd231pd    ymm2,ymm0,[rdx+r8*1+0x20]
303: vmovupd         [rdx+rsi*1+0x20],ymm2
309: add             rdx,0x40
30d: test            eax,eax
30f: jg              2e0

400: vmovupd         ymm1,[r8+rdx*1]
406: vmovupd         ymm2,[rsi+rdx*1]
40b: add             ecx,0x8
40e: vfnmadd231pd    ymm2,ymm1,ymm0
413: sub             eax,0x8
416: vmovntpd        [rsi+rdx*1],ymm2
41b: vmovupd         ymm2,[rdx+rsi*1+0x20]
421: vmovupd         ymm1,[rdx+r8*1+0x20]
428: vfnmadd231pd    ymm2,ymm1,ymm0
42d: vmovntpd        [rdx+rsi*1+0x20],ymm2
433: add             rdx,0x40
437: test            eax,eax
439: jg              400

Listing 7: Assembly of critical j-loop produced by the PGI compiler.

On our test system, this sequence of instructions yields 11.01 GFLOP/s in single threaded mode and 102.53 GFLOP/s when running with 24 threads for a 9.3x speedup (0.39x/thread).

PGC++ issues AVX2 instructions that have half the vector width of the AVX-512 instructions issued by the other compilers. Nevertheless, it manages to outperform several of the other compilers in this test.

A.5. AOCC

We compile the code using the compile line in Listing 8.

clang++ -o critical.o -c critical.cpp
        -D__ALGORITHM__=KIJ_OPT -D__AUTO__ 
        -O3 -std=c++14 -m64
        -ffast-math -fassociative-math -mfma -ffp-contract=fast
        -fopenmp=libomp
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize
        -fsave-optimization-record
        -gline-tables-only
        -gcolumn-info
        -march=skylake-avx512

Listing 8: Compile line for compiling the LU Decomposition critical.cpp source file with AOCC.

Listing 9 shows the assembly generated by AOCC for the inner loop using the Intel syntax. 5 out of the 32 available zmm registers are used.

370: vbroadcastsd    zmm0,[r9]
376: vmovupd         zmm1,[rdi-0xc0]
37d: vmovupd         zmm2,[rdi-0x80]
384: vmovupd         zmm3,[rdi-0x40]
38b: vmovupd         zmm4,[rdi]
391: vfnmadd213pd    zmm1,zmm0,[rbx-0xc0]
398: vfnmadd213pd    zmm2,zmm0,[rbx-0x80]
39f: vfnmadd213pd    zmm3,zmm0,[rbx-0x40]
3a6: vfnmadd213pd    zmm4,zmm0,[rbx]
3ac: vmovupd         [rbx-0xc0],zmm1
3b3: vmovupd         [rbx-0x80],zmm2
3ba: vmovupd         [rbx-0x40],zmm3
3c1: vmovupd         [rbx],zmm4
3c7: add             rbx,0x100
3ce: add             rdi,0x100
3d5: add             rax,0xffffffffffffffe0
3d9: jne             370

Listing 9: Assembly of critical j-loop produced by the AOCC compiler.

On our test system, this sequence of instructions yields 9.54 GFLOP/s in single threaded mode and 96.40 GFLOP/s when running with 15 threads for a 10.1x speedup (0.67x/thread).

AOCC unrolls the J-loop by a 4x, producing a pattern of instructions very similar to those produced by PGC++. A notable difference is the broadcast instruction at the top of the loop that loads the value of A[i*lda +k] into the zmm0 register.

A.6. Clang

We compile the code using the compile line in Listing 10.

clang++ -o critical.o -c critical.cpp
        -D__ALGORITHM__=KIJ_OPT -D__AUTO__
        -O3 -std=c++14 -m64 -ffast-math -fassociative-math -mfma -ffp-contract=fast
        -fopenmp=libomp
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize
        -fsave-optimization-record
        -gline-tables-only
        -gcolumn-info
        -mllvm -polly
        -mllvm -polly-vectorizer=stripmine
        -march=skylake-avx512

Listing 10: Compile line for compiling the LU Decomposition critical.cpp source file with Clang.

Listing 11 shows the assembly instructions generated by Clang for the time consuming inner col-loop using the Intel syntax. Only 5 out of the 32 available zmm registers are used.

3c0: vmovupd         zmm1,[rdi-0xc0]
3c7: vmovupd         zmm2,[rdi-0x80]
3ce: vmovupd         zmm3,[rdi-0x40]
3d5: vmovupd         zmm4,[rdi]
3db: vfnmadd213pd    zmm1,zmm0,[rbp-0xc0]
3e2: vfnmadd213pd    zmm2,zmm0,[rbp-0x80]
3e9: vfnmadd213pd    zmm3,zmm0,[rbp-0x40]
3f0: vfnmadd213pd    zmm4,zmm0,[rbp+0x0]
3f7: vmovupd         [rbp-0xc0],zmm1
3fe: vmovupd         [rbp-0x80],zmm2
405: vmovupd         [rbp-0x40],zmm3
40c: vmovupd         [rbp+0x0],zmm4
413: add             rbp,0x100
41a: add             rdi,0x100
421: add             rbx,0xffffffffffffffe0
425: jne             3c0

Listing 11: Assembly of critical j-loop produced by the LLVM compiler.

On our test system, this sequence of instructions yields 8.23 GFLOP/s in single threaded mode and 75.27 GFLOP/s when running with 15 threads for a 9.1x speedup (0.61x/thread).

The Clang produced instructions are very similar to those generated by AOCC. The only notable difference is that the Clang hoists the broadcast instruction outside the J-loop as compared to the AOCC-produced code. This change seems to impact the performance by a small amount.

A.7. Zapcc

We compile the code using the compile line in Listing 12.

zapcc++ -o critical.o -c critical.cpp
        -D__ALGORITHM__=KIJ_OPT -D__AUTO__
        -O3 -std=c++14 -m64 -ffast-math
        -fassociative-math -mfma
        -ffp-contract=fast -fopenmp=libomp
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize
        -fsave-optimization-record
        -gline-tables-only
        -gcolumn-info
        -march=skylake-avx512

Listing 12: Compile line for compiling the LU Decomposition critical.cpp source file with Zapcc.

Zapcc produces the same instructions as Clang. Listing 13 shows the assembly instructions generated by Zapcc for the J-loop using the Intel syntax. 5 out of the 32 available zmm registers are used.

3c0: vmovupd         zmm1,[rdi-0xc0]
3c7: vmovupd         zmm2,[rdi-0x80]
3ce: vmovupd         zmm3,[rdi-0x40]
3d5: vmovupd         zmm4,[rdi]
3db: vfnmadd213pd    zmm1,zmm0,[rax-0xc0]
3e2: vfnmadd213pd    zmm2,zmm0,[rax-0x80]
3e9: vfnmadd213pd    zmm3,zmm0,[rax-0x40]
3f0: vfnmadd213pd    zmm4,zmm0,[rax]
3f6: vmovupd         [rax-0xc0],zmm1
3fd: vmovupd         [rax-0x80],zmm2
404: vmovupd         [rax-0x40],zmm3
40b: vmovupd         [rax],zmm4
411: add             rax,0x100
417: add             rdi,0x100
41e: add             rbx,0xffffffffffffffe0
422: jne             3c0

Listing 13: Assembly of critical j-loop produced by the ZAPCC compiler.

On our test system, this sequence of instructions yields 8.21 GFLOP/s in single threaded mode and 74.71 GFLOP/s when running with 15 threads for a 9.1x speedup (0.61x/thread).

A.8. Takeaway

Our first computational kernel has a very simple innermost loop. Each loop iteration can be performed in a single floating point FMA instruction. Even with such a simple loop structure, we see notable differences between the instructions generated by each compiler. The performance achieved by code compiled with the different compilers varies by a factor of 1.8x (Intel C++ compiler v/s Clang/Zapcc).

Appendix B. Jacobi Solver

B.1. What does a Jacobi Solver solve?

Jacobi solvers are one of the classical methods used to solve boundary value problems (BVP) in the field of numerical partial differential equations (PDE). The Jacobi method for solving BVPs entails splitting the sparse matrix that arises from approximating the PDE using finite differences and iterating until the solution converges. Although the Jacobi method has been superseded by faster modern methods for solving PDEs, it is still important for understanding modern methods.

We use the Jacobi method to solve Poisson’s equation for electrostatics
$latex path not specified.: \Laplace\phi = -\frac{\rho}{\epsilon},$ (6)

where Δ is the Laplacian, φ is the electric potential, ρ is the electric charge density, and ε is the permeability. The solution can then be computed by iteratively updating the value of φ_i,j using

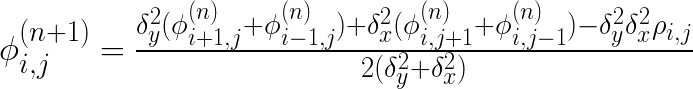$\phi_{i,j}^{(n+1)} = \frac{\delta_{y}^{2}(\phi_{i+1,j}^{(n)} + \phi_{i-1,j}^{(n)}) + \delta_{x}^{2}(\phi_{i,j+1}^{(n)} + \phi_{i,j-1}^{(n)}) - \delta_{y}^{2}\delta_{x}^{2}\rho_{i,j}}{2(\delta_{y}^{2} + \delta_{x}^{2})}$ (7)

where φ_i,j⁽ⁿ⁾ is the value of φ at the i,j-th grid point on the n-th iteration and δ is the grid spacing assuming equal spacing in the x- & y-directions.

We structure our code using methods available in C++ (object oriented programming & template programming) to test the ability of the compilers to handle more complicated code than that shown in our structure function example in the previous section. Our code uses two objects to help us write the Jacobi solver in a readable manner.

Grid objects hold a 2-dimensional grid of values using row-major storage. Each row is padded at the end so that the start of the succeeding row lies on a 64-byte boundary. These implementation details are abstracted for users of the Grid class by supplying an accessor method that makes Grid objects functors. The accessor method takes the i,j-indices of a desired memory location, maps the indices to the correct linear storage index, and provides read-write access to the value stored at that location. This object is defined as a template object where the template parameter controls the underlying datatype of the grid. We explicitly instantiate this template for double precision grid values.

Jacobi objects hold three Grid objects that are used to model the source term, solution domain, and a scratch copy of the solution domain. Jacobi objects are also template objects with the template type controlling the datatype of the individual Grid objects stored by the Jacobi object. We explicitly instantiate the Jacobi template for double precision grid values.

Jacobi objects supply a solve method that iteratively solves Equation (7) until the solution stops changing above a supplied threshold value.
Listing 14 shows our implementation of the solve method of the Jacobi class –

  template 
  int Jacobi::solve_opt(GridT tol) {
      GridT newVal, maxChange;
      int iter = 0;
      while (maxChange > tol) {
          maxChange = static_cast(0.0);
          iter += 1;
          // Perform one iteration
          int row, col;
#pragma omp parallel for private(newVal, col) reduction(max:maxChange)
          for (row = 1; row <= Ny; ++row) {
#ifndef __PGI
#pragma omp simd private(newVal) reduction(max:maxChange) linear(col:1)
#else
#pragma loop ivdep
#endif
              for (col = 1; col <= Nx; ++col) { newVal = (DySq*((*SD)(row + 1, col) + (*SD)(row - 1, col)) + DxSq*((*SD)(row, col + 1) + (*SD)(row, col - 1)) - DySqDxSq*(*S)(row, col))*OneOverTwoDySqPlusDxSq; maxChange = (std::fabs(newVal - (*D)(row, col)) > maxChange)
                              ? std::fabs(newVal - (*D)(row, col)) : maxChange;
                  (*D)(row, col) = newVal;
              }
          }
          // Swap the ScratchDomain storage with the storage of the Domain.
          (*D).swapStorage((*SD));
      } // end while
      // Swap the ScratchDomain storage with the storage of the Domain.
      (*D).swapStorage((*SD));
      return iter;
  }

Listing 14: Jacobi Solver implementation.

The workload in this function consists of a while-loop that performs iterations of Equation (7) along with two nested for-loops that compute the domain update.

The domain update is performed in three steps. At the beginning of the update, we set the variable maxChange to 0. For each location in the domain, we compute the new value of the location in the variable newVal using the values in the scratch domain. We update maxChange with the difference of newVal and the existing value of the domain location if said difference is greater than maxChange, i.e., we use maxChange to track the largest update to the domain. Finally, we replace the existing value of the domain location with newVal and move to the next location. At the end of the domain update, we switch the domain with the scratch domain, i.e., we perform the updates out-of-place. Our exit condition for the while-loop tests if the largest change in the solution domain maxChange has dropped below the user input tolerance. The function returns the number of while-loop iterations performed.

Three factors are crucial for achieving good performance in this test. We call the accessor method of the Grid objects multiple times from inside the innermost col-loop. Therefore, we must creates a version of the accessor method that can process multiple arguments using SIMD instructions from a single invocation from a SIMD loop. We do this by declaring the method with the OpenMP directive #pragma omp declare simd. This directive is not available in versions of OpenMP before OpenMP 4.0.

We wish to vectorize the col-loop to achieve good performance. When running concurrently, each iteration of this loop must retain a private copy of newVal. We also require a reduction over the value of maxChange. We can achieve both behaviors using the private and reduction clauses to the #pragma omp simd directive. Both clauses become available along with the #pragma omp simd directive in OpenMP 4.0.

Parallelizing the calculation over the row-loop requires similar reduction & private clauses to be applied to a #pragma omp parallel for directive that acts on the row-loop. Both clauses and the directive itself are available in OpenMP versions older than 4.0.

We expect the non-OpenMP 4.0 compliant PGC++ 17.4 Community Edition compiler to produce parallelized but un-vectorized code in the absence of PGI-specific directives. OpenMP 4.0 SIMD support was introduced in the PGI compiler starting with version 17.7. We perform our tests with the Community Edition that lacks OpenMP 4.0 SIMD support.

Each iteration of the while-loop performs a total of 9n² floating point operations where n is the number of rows or columns in the solution domain. The number of while-loop iterations N_iter performed to reach convergence is returned by the solve method. Hence the total number of floating point operations performed is 9n²N_iter.

We discuss the assembly code generated by each compiler to gain further insight.

B.2. Intel C++ compiler

We compile the code using the compile line in Listing 15.

icpc -o critical.o -c critical.cpp
     -D__ALGORITHM__=SOLVE_OPT -D__AUTO__
     -O3 -Wall -std=c++14 -ipo
     -qopenmp -qopenmp-simd
     -qopt-report=5
     -qopt-assume-safe-padding
     -xCORE-AVX512 -qopt-zmm-usage=high
icpc -o jacobiSolve grid.o critical.o jacobi.o jacobiSolve.o
     -ipo -liomp5 -lm

Listing 15: Compile & link lines for compiling the Jacobi solver critical.cpp source file with Intel C++ compiler.

Listing 16 shows the assembly instructions generated by Intel C++ compiler for the time consuming inner col-loop using the Intel syntax. The assembly generated for the inner loop consists of a mix of primarily AVX-512F instructions along with some vector AX2 instructions for computing a mask, and a handful of scalar x86 instructions for managing the loop. 14 out of 32 zmm registers and 2 out of 16 ymm registers are used in the loop.

402cd5: vpcmpgtd     k1,ymm11,ymm12
402cdb: vpaddd       ymm12,ymm12,ymm1
402cdf: vmovupd      zmm16{k1}{z},[rdx+rcx*8+0x10]
402cea: vmovupd      zmm17{k1}{z},[rdx+rcx*8]
402cf1: vmovupd      zmm14{k1}{z},[r15+rcx*8+0x8]
402cfc: vmovupd      zmm15{k1}{z},[r10+rcx*8+0x8]
402d07: vmovupd      zmm20{k1}{z},[r14+rcx*8+0x8]
402d12: vmovupd      zmm22{k1}{z},[rdi+rcx*8+0x8]
402d1d: vaddpd       zmm18,zmm16,zmm17
402d23: vaddpd       zmm19,zmm14,zmm15
402d29: vmulpd       zmm21,zmm8,zmm18
402d2f: vfmadd231pd  zmm21,zmm19,zmm9
402d35: vfnmadd231pd zmm21,zmm20,zmm7
402d3b: vmulpd       zmm24,zmm10,zmm21
402d41: vfmsub231pd  zmm22,zmm21,zmm10
402d47: vmovupd      [rdi+rcx*8+0x8]{k1},zmm24
402d52: add          rcx,0x8
402d56: vpandq       zmm23,zmm6,zmm22
402d5c: vmaxpd       zmm13{k1},zmm23,zmm13
402d62: cmp          rcx,rax
402d65: jb           402cd5

Listing 16: Assembly of critical col-loop produced by the Intel compiler.

On our test system, this sequence of instructions yields 15.04 GFLOP/s in single threaded mode and 102.55 GFLOP/s when running with 14 threads for a 6.8x speedup (0.48x/thread).

An analysis of the assembly shows that Intel C++ compiler manages to successfully vectorize the innermost col-loop by using masked memory access operations. Intel C++ compiler loads the values of φ⁽ⁿ⁾_i,j-1, φ⁽ⁿ⁾_i,j+1, etc., using a mask computed to load only selected memory locations into zmm registers. The computation of newVal is then built up step-by-step with the final update being computed by line 402d3b in the zmm24 register. The next few instructions compute the difference between the current grid value and the updated grid value, compare the difference to the running maximum difference and write the updated value into the grid. This sequence of instructions uses 6 memory reads and 1 memory write to update each grid point.

B.3. G++

We compile the code using the compile line in Listing 17.

g++ -o critical.o -c critical.cpp -D__ALGORITHM__=SOLVE_OPT -D__AUTO__
    -O3 -Wall -std=c++14 -m64 -fipa-pta -flto -ffast-math -fassociative-math
    -ftree-vectorize -ftree-vectorizer-verbose=0 -fopenmp -fopenmp-simd
    -fopt-info-all=jacobiSolve.gnurpt -march=skylake-avx512

g++ -o jacobiSolve -flto -O3 -fipa-pta -ffast-math -fassociative-math 
    -ftree-vectorize grid.o critical.o jacobi.o jacobiSolve.o -lgomp -lm

Listing 17: Compile & link lines for compiling the Jacobi solver critical.cpp source file with G++.

Listing 18 shows the assembly instructions generated by G++ for the inner loop using the Intel syntax. G++ also successfully vectorizes the loop, using 6 out of 32 zmm registers to perform the computation.

402ab0: vmovupd      zmm3,[r8+rax*1]
402ab7: vaddpd       zmm3,zmm3,[r9+rax*1]
402abe: add          edx,0x1
402ac1: vbroadcastsd zmm0,[r14+0x58]
402ac8: vmovupd      zmm1,[r11+rax*1]
402acf: vaddpd       zmm1,zmm1,[r10+rax*1]
402ad6: vbroadcastsd zmm2,[r14+0x60]
402add: vmulpd       zmm3,zmm3,zmm0
402ae3: vbroadcastsd zmm0,[r14+0x50]
402aea: vfmadd132pd  zmm0,zmm3,zmm1
402af0: vfnmadd132pd zmm2,zmm0,[rsi+rax*1]
402af7: vbroadcastsd zmm0,[r14+0x68]
402afe: vmulpd       zmm0,zmm2,zmm0
402b04: vsubpd       zmm1,zmm0,[rcx+rax*1]
402b0b: vandpd       zmm1,zmm1,zmm6
402b11: vmovupd      [rcx+rax*1],zmm0
402b18: vmaxpd       zmm8,zmm8,zmm1
402b1e: add          rax,0x40
402b22: cmp          [rbp-0x74],edx
402b25: ja           402ab0

Listing 18: Assembly of critical col-loop produced by the GNU compiler.

On our test system, this sequence of instructions yields 12.80 GFLOP/s in single threaded mode and 74.44 GFLOP/s when running with 9 threads with a 5.8x speedup (0.64x/thread).

G++ also manages to successfully vectorize the inner col-loop but uses a very different strategy to compute the grid update as compared to Intel C++ compiler. G++ is very parsimonious when using zmm registers as compared to Intel C++ compiler, using only 6 out of a total of 32 available zmm registers. To compensate for the low register usage, G++ issues more memory operations, using 10 memory reads and 1 memory write in this loop. A key difference is that 4 out of the 10 memory read operations are vbroadcastsd instructions that can only be executed on 1 port (port 5) on the Skylake microarchitecture (see this manual). In contrast, the vmovupd memory read instructions issued by Intel C++ compiler can be executed on any of 4 different ports (ports 0, 1, 5, or 6). The throughput of the vmovupd is much higher because of the greater number of execution units that are capable of being assigned this operation.

We believe that the extra memory operations performed by G++, some of which can only be executed on one port inside the CPU, causes the code compiled by G++ to be slower as compared to that compiled by Intel C++ compiler.

B.4. AOCC

We compile the code using the compile line in Listing 19.

clang++ -o critical.o -c critical.cpp -D__ALGORITHM__=SOLVE_OPT -D__AUTO__
        -O3 -Wall -std=c++14 -m64 -flto -ffast-math -fassociative-math -mfma 
        -ffp-contract=fast -fopenmp=libomp -Rpass-analysis=loop-vectorize
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -fsave-optimization-record -gline-tables-only -gcolumn-info
        -march=skylake-avx512

clang++ -o jacobiSolve -flto -fuse-ld=lld
        grid.o critical.o jacobi.o jacobiSolve.o -lomp -lm

Listing 19: Compile & link lines for compiling the Jacobi solver critical.cpp source file with AOCC.

Listing 20 shows the assembly generated by AOCC for the inner loop using the Intel syntax.

2012d0: vmovsd       xmm3,[rsi+rcx*8]
2012d5: vaddsd       xmm3,xmm3,[rdx+rcx*8]
2012da: vmulsd       xmm3,xmm3,[rbp+0x50]
2012df: vmovsd       xmm4,[rdi+rcx*8-0x10]
2012e5: vaddsd       xmm4,xmm4,[rdi+rcx*8]
2012ea: vfmadd132sd  xmm4,xmm3,[rbp+0x58]
2012f0: vmovsd       xmm3,[rax+rcx*8]
2012f5: vfnmadd132sd xmm3,xmm4,[rbp+0x60]
2012fb: vmulsd       xmm3,xmm3,[rbp+0x68]
201300: vsubsd       xmm4,xmm3,[rbx+rcx*8]
201305: vandpd       xmm4,xmm4,xmm1
201309: vmaxsd       xmm2,xmm4,xmm2
20130d: vmovsd       [rbx+rcx*8],xmm3
201312: lea          rcx,[rcx+0x1]
201316: cmp          r11,rcx
201319: jne          2012d0

Listing 20: Assembly of critical col-loop produced by the AOCC compiler.

On our test system, this sequence of instructions yields 4.72 GFLOP/s in single threaded mode and 58.16 GFLOP/s when running with 44 threads for a 12.3x speedup (0.28x/thread).

AOCC has trouble with the reduce clause and is unable to vectorize the col-loop when performing the inter-procedural optimizations (compiler diagnostic: value that could not be identified as reduction is used outside the loop). Instead, the compiler issues pure scalar AVX instructions. As a direct consequence of not vectorizing the loop, the AOCC produced code runs almost 4x slower than the code produced by Intel C++ compiler when run with a single thread. Although the expected theoretical drop in performance between scalar & AVX-512 code is 8x, the Intel C++ compiler-code uses masked instructions, reducing the amount of useful work per loop iteration.

When run with more than a single thread of execution, the AOCC-produced code running with 44 threads is only ~0.57x slower than the Intel C++ compiler-produced code running with 14 threads. While the overall performance is improved relative to Intel C++ compiler, AOCC has the poorest gain per extra thread of execution. We hypothesize that the improvement in relative performance arises because of differences in the OpenMP implementation provided by the Intel and AMD OpenMP libraries.

We believe that the inability of AOCC to vector instructions for the innermost col-loop hurts the performance of the AOCC-generated code.

B.5. Clang

We compile the code using the compile line in Listing 21.

clang++ -o critical.o -c critcal.cpp -D__ALGORITHM__=SOLVE_OPT -D__AUTO__
        -O3 -Wall -std=c++14 -stdlib=libc++ -fopenmp=libomp
        -m64 -flto -ffast-math -fassociative-math -mfma -ffp-contract=fast
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize
        -fsave-optimization-record -gline-tables-only -gcolumn-info
        -mllvm -polly -mllvm -polly-vectorizer=stripmine -march=skylake-avx512

clang++ -o jacobiSolve -flto -fuse-ld=lld
        grid.o critical.o jacobi.o jacobiSolve.o -lomp -lm

Listing 21: Compile & link lines for compiling the Jacobi solver critical.cpp source file with Clang.

Listing 22 shows the assembly generated by Clang for the inner loop using the Intel syntax.

2012e0: vmovsd       xmm3,[rcx+rsi*8]
2012e5: vaddsd       xmm3,xmm3,[rdx+rsi*8]
2012ea: vmovsd       xmm4,[rdi+rsi*8-0x10]
2012f0: vaddsd       xmm4,xmm4,[rdi+rsi*8]
2012f5: vmovhpd      xmm4,xmm4,[rax+rsi*8]
2012fa: vmulpd       xmm4,xmm4,[rbp+0x58]
2012ff: vfmadd132sd  xmm3,xmm4,[rbp+0x50]
201305: vpermilpd    xmm4,xmm4,0x1
20130b: vsubsd       xmm3,xmm3,xmm4
20130f: vmulsd       xmm3,xmm3,[rbp+0x68]
201314: vsubsd       xmm4,xmm3,[rbx+rsi*8]
201319: vandpd       xmm4,xmm4,xmm1
20131d: vmaxsd       xmm2,xmm4,xmm2
201321: vmovsd       [rbx+rsi*8],xmm3
201326: lea          rsi,[rsi+0x1]
20132a: cmp          r11,rsi
20132d: jne          2012e0

Listing 22: Assembly of critical col-loop produced by the LLVM compiler.

On our test system, this sequence of instructions yields 4.39 GFLOP/s in single threaded mode and 42.31 GFLOP/s when running with 20 threads for a 9.6x speedup (0.48x/thread).

Like AOCC, Clang is unable to properly vectorize the inner col-loop when performing interprocedural optimizations. Instead, Clang issues scalar AVX instructions to perform the loop operations. Unlike AOCC, the Clang-generated code performs a small number of operations using vector instructions starting with the load instruction on line 2012f5 that loads the double precision value at the location held in rax+rsi*8 into the upper half of the zmm4 register, filling it with 2 double precision values. However, in practice, this approach does not work as well as that adopted by AOCC, yielding slightly poorer performance when run with a single thread.

B.6. Zapcc

We compile the code using the compile line in Listing 23.

zapcc++ -o critical.o -c critical.cpp -D__ALGORITHM__=SOLVE_OPT -D__AUTO__
        -O3 -Wall -std=c++14 -fopenmp=libomp
        -m64 -flto -ffast-math -fassociative-math -mfma -ffp-contract=fast
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize -fsave-optimization-record
        -gline-tables-only -gcolumn-info -march=skylake-avx512

zapcc++ -o jacobiSolve -flto -fuse-ld=lld
        grid.o critical.o jacobi.o jacobiSolve.o -lomp -lm

Listing 23: Compile & link lines for compiling the Jacobi solver critical.cpp source file with Zapcc.

Listing 24 shows the assembly instructions generated by Zapcc for the inner loop using the Intel syntax.

2012e0: vmovsd       xmm3,[rcx+rsi*8]
2012e5: vaddsd       xmm3,xmm3,[rdx+rsi*8]
2012ea: vmovsd       xmm4,[rdi+rsi*8-0x10]
2012f0: vaddsd       xmm4,xmm4,[rdi+rsi*8]
2012f5: vmovhpd      xmm4,xmm4,[rax+rsi*8]
2012fa: vmulpd       xmm4,xmm4,[rbp+0x58]
2012ff: vfmadd132sd  xmm3,xmm4,[rbp+0x50]
201305: vpermilpd    xmm4,xmm4,0x1
20130b: vsubsd       xmm3,xmm3,xmm4
20130f: vmulsd       xmm3,xmm3,[rbp+0x68]
201314: vsubsd       xmm4,xmm3,[rbx+rsi*8]
201319: vandpd       xmm4,xmm4,xmm1
20131d: vmaxsd       xmm2,xmm4,xmm2
201321: vmovsd       [rbx+rsi*8],xmm3
201326: lea          rsi,[rsi+0x1]
20132a: cmp          r11,rsi
20132d: jne          2012e0

Listing 24: Assembly of critical col-loop produced by the ZAPCC compiler.

On our test system, this sequence of instructions yields 4.40 GFLOP/s in single threaded mode and 41.40 GFLOP/s when running with 21 threads for a 9.4x speedup (0.45x/thread).

Zapcc produces the exact same set of instructions as Clang for this computational kernel. The observed performance is very similar with the difference being attributable to runtime statistical variations.

B.7. PGC++

We compile the code using the compile line in Listing 25.

pgc++ -o critical.o -c critical.cpp -D__ALGORITHM__=SOLVE_OPT -D__AUTO__
      -O3 -Minform=warn -std=c++11 -tp=haswell -fast -O4
      -Mipa=fast,align,inline -fma
      -Mvect=altcode,gather,simd,assoc,cachesize:32768
      -Msmart -Mfma -Mcache_align
      -Mipa=all -Mmovnt -mp -Mquad
      -Msafeptr=all -Minfo=all -Mnoprefetch

pgc++ -o jacobiSolve -Mipa=fast,align,inline -mp=bind
      grid.o critical.o jacobi.o jacobiSolve.o -lstdc++ -lpgmp -lm

Listing 25: Compile & link lines for compiling the Jacobi solver critical.cpp source file with PGC++.

Listing 26 shows the assembly instructions generated by PGC++ for the time consuming inner col-loop using the Intel syntax. Only 4 out of the 16 available xmm registers are used.

404208: vmovsd       xmm1,[rsi]
40420c: mov          r14,[rbp-0x18]
404210: vmovsd       xmm3,[rdx-0x10]
404215: sub          r9,0x1
404219: vaddsd       xmm2,xmm1,[rdi]
40421d: vmulsd       xmm1,xmm2,[r14+0x50]
404223: vaddsd       xmm2,xmm3,[rdx]
404227: add          rsi,0x8
40422b: vfmadd132sd  xmm2,xmm1,[r14+0x58]
404231: vmovsd       xmm1,[r14+0x60]
404237: vfnmadd132sd xmm1,xmm2,[r8]
40423c: vmulsd       xmm2,xmm1,[r14+0x68]
404242: add          r8,0x8
404246: vsubsd       xmm3,xmm2,[rcx]
40424a: vmovsd       [rcx],xmm2
40424e: vandpd       xmm1,xmm3,[rip+0xfffffffffffffe2a]
404256: add          rcx,0x8
40425a: vmaxsd       xmm0,xmm0,xmm1
40425e: add          rdi,0x8
404262: add          rdx,0x8
404266: test         r9,r9
404269: jg           404208

Listing 26: Assembly of critical col-loop produced by the PGI compiler.

On our test system, this sequence of instructions yields 4.28 GFLOP/s in single threaded mode and 30.70 GFLOP/s when running with 13 threads for a 7.2x speedup (0.55x/thread).

PGC++ 17.4 (Community Edition) is not OpenMP 4.0 compliant and does not accept the OpenMP 4.0 directive #pragma omp simd. Instead, we supply the PGI specific compiler directive #pragma loop ivdep to inform the compiler that the loop is safe to vectorize. Notice though that this directive has no ability to inform the compiler that we wish to perform a reduction over the maxChange variable. The compiler fails to vectorize the loop emitting the un-helpful diagnostic: potential early exits.

B.8. Takeaway

Our second computational kernel tests the ability of each compiler to peer through the haze of abstraction and produce optimal code. Given the same information, only two compilers manage to successfully vectorize the innermost loop in the Jacobi solver.

Large scientific/engineering/financial codes can contain dense layers of abstraction designed to let the programmer reason about the program. The abstraction can take a significant portion of the project time to develop. It is crucial for the compiler used for such development to be able to optimize non-HPC modern C++ code written for readability and maintainability.

In the second computational kernel, the difference in performance between the best and worst compilers jumps to 3.5x (Intel C++ compiler v/s PGC++).

Appendix C. Structure Function

C.1. What is the Structure Function?

The autocorrelation function is a valuable diagnostic for studying time series data. Polynomial trends in the time series data can make direct estimation of the autocorrelation function difficult. Structure functions can be used as a proxy for the autocorrelation function when studying time-series data since they possess the proprty that an n-th order structure function is insensitive to polynomial trends of order n-1 in the time series.

Given a time series A(t), the first-order structure function is defined as

$\mathrm{SF}(\tau) = \langle[A(t + \tau) - A(t)]^{2}\rangle_{t},$ (8)

where <A>_t is the expectation value of the random variable A over the epochs t.

The time series A may not be uniformly sampled making direct estimation of the structure function using Equation (8) difficult. Non-uniformly sampled time series can be registered onto a uniform grid in time by using a mask to track missing observations. Given n observations A_i on a uniform gridding with timestep δt with binary mask M_i storing 1 at observed timesteps & 0 at missing observations, Equation (8) can be expressed as

$\mathrm{SF}(o) = \frac{\sum_{i} M_{i + o}M_{i}[A_{i + o} - A_{i}]^{2}}{\sum_{i} M_{i + \tau}M_{i}},$ (9)

with 0≤o≤n-1 and τ=oδt.

Listing 27 shows our implementation of Equation (9). Our implementation assumes that the input data and mask arrays A & M are padded with 0s for 32 entries past the end of the arrays. The padding allows us to write simpler loops inside the main loop and will be explained in more detail below.

  void SF_compute_oblkio_opt(int const n, double const * const A,
                             double const * const M, double * const SF) {
#if defined(__PGI)
#pragma routine safe
#endif
    const int c = BLOCK_SIZE;
#pragma omp parallel for schedule(dynamic)
    for (int oblk = 0; oblk < n/c; ++oblk) {
      double SFTemp_private[c];
      double countSFTemp_private[c];
      for (int ctr = 0; ctr < c; ++ctr) {
        SFTemp_private[ctr] = 0.0;
        countSFTemp_private[ctr] = 0.0;
      } // end for ctr
      register double * S0 = SFTemp_private + 0*8;
      register double * S1 = SFTemp_private + 1*8;
      register double * S2 = SFTemp_private + 2*8;
      register double * S3 = SFTemp_private + 3*8;
      register double * c0 = countSFTemp_private + 0*8;
      register double * c1 = countSFTemp_private + 1*8;
      register double * c2 = countSFTemp_private + 2*8;
      register double * c3 = countSFTemp_private + 3*8;
      for (int i = 0; i < n - oblk*c; ++i) {
        double MVal0, MVal1, MVal2, MVal3;
#if defined(__PGI)
#pragma loop ivdep
#else
#pragma omp simd private(MVal0, MVal1, MVal2, MVal3)
#endif
        for (int v = 0 ; v < 8; v++) {
          MVal0 = M[i + oblk*c + 0*8 + v]*M[i];
          S0[v] += MVal0*(A[i + oblk*c + 0*8 + v] - A[i])
                   *(A[i + oblk*c + 0*8 + v] - A[i]);
          c0[v] += MVal0;
          MVal1 = M[i + oblk*c + 1*8 + v]*M[i];
          S1[v] += MVal1*(A[i + oblk*c + 1*8 + v] - A[i])
                   *(A[i + oblk*c + 1*8 + v] - A[i]);
          c1[v] += MVal1;
          MVal2 = M[i + oblk*c + 2*8 + v]*M[i];
          S2[v] += MVal2*(A[i + oblk*c + 2*8 + v] - A[i])
                   *(A[i + oblk*c + 2*8 + v] - A[i]);
          c2[v] += MVal2;
          MVal3 = M[i + oblk*c + 3*8 + v]*M[i];
          S3[v] += MVal3*(A[i + oblk*c + 3*8 + v] - A[i])
                   *(A[i + oblk*c + 3*8 + v] - A[i]);
          c3[v] += MVal3;
        } // end for v
      } // end for i
      for (int ctr = 0; ctr < c; ++ctr) {
        SF[oblk*c + ctr] = SFTemp_private[ctr]/countSFTemp_private[ctr];
      } } } // end for ctr, blk and function

Listing 27: Structure function implementation.

We compute the structure function for entry SF[o] in blocks of size c = BLOCK_SIZE. Thus our outer oblk-loop loops over n/c blocks of o with each block being of size c.

We parallelize our structure function calculation over the oblk-loop, i.e., each thread evaluates the structure function for a different block of o-values.

The number of computations required to compute SF[o] drops as o increases. Therefore the workload in each block also reduces as oblk increases. We use ‘dynamic’ OpenMP scheduling to optimally balance the computational workload across all the available threads.

The value of BLOCK_SIZE has to be tuned for each system. We find that on our 2-socket Intel Xeon Platinum 8168 test platform, setting BLOCK_SIZE = 32 gives us good results.

We use the temporary arrays SFTemp_private & countSFTemp_private to accumulate the contribution to the structure function from each term in the summation in the numerator and denominator of Equation (9). Since the length of these temporary arrays (BLOCK_SIZE) is known at compile time, we declare the arrays on the function stack.

When the calculation is performed in parallel, each OpenMP thread possesses an individual stack and the SFTemp_private & countSFTemp_private arrays are local to the stack of each OpenMP thread. Since the arrays are relatively small compared to the OpenMP stacksize, the temporary arrays are located far away from each other in memory. This makes false sharing almost negligible.

The i-loop ranges between 0 and n-oblk*c. We unroll the innermost o-loop by a factor of 4 and rewrite it as a loop over the variable v. Since A and M are padded with 0s for 32 entries after the end of each array, we can safely index each array inside the innermost v-loop.

We vectorize the v-loop by issuing the OpenMP directive #pragma omp simd for Intel C++ compiler, G++, and the LLVM-based compilers. For PGC++ we issue the PGI-specific directive #pragma loop ivdep. As confirmed by the optimization reports from each compiler and by an examination of the assembly, this is sufficient to let each compiler generate vectorized instructions for the v-loop.

Each iteration of the o-loop performs a total of 6 floating point operations. Since the algorithm runs over all unique pairs of observations A_i, there are a total of 3n(n-1) useful floating point operations in the v-loop followed by another n division operations in the final loop for a total of 3n²+2n floating point operations to compute the structure function using this algorithm.

Recall that the theoretical peak performance for purely FMA double precision computations on a single core is P_{×1^FMA=112 GFLOP/s for our test system. The Intel & AMD compilers manage to reach ~57 GFLOP/s which is about 0.5x the theoretical FMA peak and slightly higher than the P_×1=56&nsbp;GFLOP/s non-FMA peak. The assembly generated by these compilers suggests that the gap in performance between the theoretical peak and the achieved performance with these compilers is due to the combination of the presence of mandatory load instructions as well as the presence of non-FMA computations in the final code.

When executing with multiple threads of instructions both the Intel & AMD compilers manage to reach ~2 TFLOP/s on our test system. This level of performance is ~0.5x the theoretical FMA peak of 3.84 TFLOP/s, which shows that performance scales linearly with the number of cores on this computational kernel, i.e., the kernel is compute bound.

We discuss the assembly code generated by each compiler to gain further insight.

C.2. Intel C++ compiler

We compile the code using the compile line in Listing 28.

icpc -o critical.o -c critical.cpp
     -D__ALGORITHM__=OBLKIO_OPT -D__AUTO__
     -O3 -std=c++14
     -qopenmp -qopenmp-simd
     -qopt-report=5
     -qopt-assume-safe-padding
     -xCORE-AVX512
     -qopt-zmm-usage=high

Listing 28: Compile line for compiling the structure function critical.cpp source file with Intel C++ compiler.

Listing 29 shows the assembly instructions generated by Intel C++ compiler for the inner v-loop using the Intel syntax. The assembly generated for the inner loop consists of a mix of primarily AVX-512F instructions along with a handful of scalar x86 instructions for managing the loop. Correspondingly, the zmm registers are used heavily (31 out of 32 registers used).

32d: vmovups       zmm13,[rcx+r9*8]
334: vmovups       zmm18,[rcx+r9*8+0x40]
33c: vmovups       zmm23,[rcx+r9*8+0x80]
344: vmovups       zmm29,[rcx+r9*8+0xc0]
34c: vmovups       zmm9,[rbx+r9*8]
353: vmovups       zmm14,[rbx+r9*8+0x40]
35b: vmovups       zmm19,[rbx+r9*8+0x80]
363: vmovups       zmm24,[rbx+r9*8+0xc0]
36b: vbroadcastsd  zmm30,[r13+r9*8+0x0]
373: vbroadcastsd  zmm25,[r12+r9*8]
37a: vmulpd        zmm10,zmm30,zmm13
380: vmulpd        zmm15,zmm30,zmm18
386: vmulpd        zmm20,zmm30,zmm23
38c: vmulpd        zmm26,zmm30,zmm29
392: vfmadd231pd   zmm7,zmm13,zmm30
398: vfmadd231pd   zmm5,zmm18,zmm30
39e: vfmadd231pd   zmm3,zmm23,zmm30
3a4: vfmadd231pd   zmm1,zmm29,zmm30
3aa: vsubpd        zmm11,zmm9,zmm25
3b0: vsubpd        zmm16,zmm14,zmm25
3b6: vsubpd        zmm21,zmm19,zmm25
3bc: vsubpd        zmm27,zmm24,zmm25
3c2: vmulpd        zmm12,zmm10,zmm11
3c8: vmulpd        zmm17,zmm15,zmm16
3ce: vmulpd        zmm22,zmm20,zmm21
3d4: vmulpd        zmm28,zmm26,zmm27
3da: vfmadd231pd   zmm8,zmm11,zmm12
3e0: vfmadd231pd   zmm6,zmm16,zmm17
3e6: vfmadd231pd   zmm4,zmm21,zmm22
3ec: vfmadd231pd   zmm2,zmm27,zmm28
3f2: inc           r9
3f5: cmp           r9,r15
3f8: jb            32d

Listing 29: Assembly of critical o-loop produced by the Intel compiler.

On our test system, this sequence of instructions yields 57.40 GFLOP/s in single threaded mode and 2050.96 GFLOP/s when running with 48 threads.

Intel C++ compiler prefers to use almost every available AVX-512 register. The benefit of doing so is that the resulting assembly instructions can be easily reordered by the CPU since there is minimal dependency between instructions. As a result, there are only 10 memory accesses per v-loop iteration, all of which consist of memory reads.

An analysis of the assembly shows that Intel C++ compiler chooses to compute the mask product twice. Although this seems redundant, it allows the compiler to issue an extra FMA instruction instead of a multiply instruction. This decision makes logical sense on the older Broadwell microarchitecture. On the Broadwell microarchitecture, FMA instructions have a latency of 0.5 cycles as compared to a 1 cycle latency for multiply instructions. On the Skylake microarchitecture, all the basic AVX-512 floating point operations ((v)addp*, (v)mulp*, (v)fmaddXXXp*, etc.) have the same throughput of 0.5 cycles/instruction. See Tables 2-2 & 2-3 in this manual for more details.

C.3. AOCC

We compile the code using the compile line in Listing 30.

clang++ -o critical.o -c critical.cpp -D__ALGORITHM__=OBLKIO_OPT -D__AUTO__
        -O3 -std=c++14 -m64 -fopenmp=libomp
        -ffast-math -mavx2 -fassociative-math -mfma -ffp-contract=fast
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize -fsave-optimization-record
        -gline-tables-only -gcolumn-info -march=skylake-avx512

Listing 30: Compile line for compiling the structure function critical.cpp source file with AOCC..

Listing 31 shows the assembly generated by AOCC for the inner loop using the Intel syntax.

2b0: vmovapd       zmm8,zmm7
2b6: vmovapd       zmm7,zmm4
2bc: vmovapd       zmm9,zmm5
2c2: vmovapd       zmm10,zmm6
2c8: vbroadcastsd  zmm6,[rdi+r15*8]
2cf: vbroadcastsd  zmm11,[rbx+r15*8]
2d6: vmulpd        zmm5,zmm6,[r14+r15*8-0xc0]
2de: vmovupd       zmm4,[rsi+r15*8-0xc0]
2e6: vsubpd        zmm4,zmm4,zmm11
2ec: vmulpd        zmm4,zmm4,zmm4
2f2: vfmadd213pd   zmm4,zmm5,zmm7
2f8: vaddpd        zmm2,zmm2,zmm5
2fe: vmulpd        zmm7,zmm6,[r14+r15*8-0x80]
306: vmovupd       zmm5,[rsi+r15*8-0x80]
30e: vsubpd        zmm5,zmm5,zmm11
314: vmulpd        zmm5,zmm5,zmm5
31a: vfmadd213pd   zmm5,zmm7,zmm9
320: vaddpd        zmm1,zmm1,zmm7
326: vmulpd        zmm9,zmm6,[r14+r15*8-0x40]
32e: vmovupd       zmm7,[rsi+r15*8-0x40]
336: vsubpd        zmm7,zmm7,zmm11
33c: vmulpd        zmm7,zmm7,zmm7
342: vfmadd213pd   zmm7,zmm9,zmm8
348: vaddpd        zmm3,zmm3,zmm9
34e: vmulpd        zmm8,zmm6,[r14+r15*8]
355: vmovupd       zmm6,[rsi+r15*8]
35c: vsubpd        zmm6,zmm6,zmm11
362: vmulpd        zmm6,zmm6,zmm6
368: vfmadd213pd   zmm6,zmm8,zmm10
36e: vaddpd        zmm0,zmm0,zmm8
374: add           r15,0x1
378: cmp           r15,rdx
37b: jl            2b0

Listing 31: Assembly of critical o-loop produced by the AOCC compiler.

On our test system, this sequence of instructions yields 57.24 GFLOP/s in single threaded mode and 1987.35 GFLOP/s when running with 96 threads.

AOCC is very parsimonious when using only 12 zmm registers. It manages to be frugal by shuffling values around rather than writing them to memory. For example, rather than writing out the values of the running sums for the numerator and denominator of Equation (9), AOCC retains these sums in registers. Line 2f2 uses the current value of the running sum of the numerator Σ_iM[i]M[i+o](A[i+o]-A[i])² in the zmm7 register and puts the updated value into the zmm4 register. On the next loop iteration, line 2b6 moves the running sum from the zmm4 register into the zmm7 register making it ready for line 2f2 to re-use. Other such examples can be found by looking through Listing 31. A technique known as Zero-Latency MOV instructions allows the CPU to perform most register to register data moves in the front-end of the CPU and have no impact on the final performance of the code (see this manual). Therefore, each v-loop iteration performs 10 memory reads with no writes to memory.

AOCC & Intel C++ compiler have different but ultimately equivalent approaches to handling the partially-unrolled v-loop. Intel C++ compiler uses a large number of registers to hold intermediate results such as the running sums in the numerator and denominator in order to minimize memory operations. AOCC manages to achieve similar performance while using a smaller number of registers by moving results around between registers. By minimizing memory operations, both codes manage to achieve very good performance in this benchmark.

C.4. G++

We compile the code using the compile line in Listing 32.

g++ -o critical.o -c critical.cpp
    -D__ALGORITHM__=OBLKIO_OPT -D__AUTO__
    -O3 -std=c++14 -m64
    -ffast-math -fassociative-math 
    -ftree-vectorize -ftree-vectorizer-verbose=0
    -fopenmp -fopenmp-simd
    -fopt-info-all=sfComp.o.gnurpt
    -march=skylake-avx512

Listing 32: Compile line for compiling the structure function critical.cpp source file with G++..

Listing 33 shows the assembly instructions generated by G++ for the time consuming inner v-loop using the Intel syntax. Only 7 out of the 32 available zmm registers are used.

130: vbroadcastsd  zmm1,[rax+rdx*1]
137: vmulpd        zmm3,zmm1,[rax]
13d: add           rax,0x8
141: add           rcx,0x8
145: vbroadcastsd  zmm0,[rcx+rdx*1-0x8]
14d: vmovupd       zmm2,[rcx-0x8]
157: vsubpd        zmm2,zmm2,zmm0
15d: vaddpd        zmm6,zmm6,zmm3
163: vmulpd        zmm4,zmm2,zmm3
169: vfmadd231pd   zmm5,zmm4,zmm2
16f: vmovupd       zmm2,[rcx+0x38]
179: vmulpd        zmm4,zmm1,[rax+0x38]
183: vsubpd        zmm2,zmm2,zmm0
189: vmulpd        zmm3,zmm2,zmm4
18f: vaddpd        zmm4,zmm4,[rbp-0xf0]
199: vfmadd213pd   zmm2,zmm3,[rbp-0x1f0]
1a3: vmovapd       [rbp-0xf0],zmm4
1ad: vmulpd        zmm4,zmm1,[rax+0x78]
1b7: vmovapd       [rbp-0x1f0],zmm2
1c1: vmovupd       zmm2,[rcx+0x78]
1cb: vsubpd        zmm2,zmm2,zmm0
1d1: vmulpd        zmm3,zmm2,zmm4
1d7: vaddpd        zmm4,zmm4,[rbp-0xb0]
1e1: vfmadd213pd   zmm2,zmm3,[rbp-0x1b0]
1eb: vmovapd       [rbp-0xb0],zmm4
1f5: vmovapd       [rbp-0x1b0],zmm2
1ff: vmulpd        zmm2,zmm1,[rax+0xb8]
209: vmovupd       zmm1,[rcx+0xb8]
213: vsubpd        zmm0,zmm1,zmm0
219: vmulpd        zmm1,zmm0,zmm2
21f: vfmadd213pd   zmm0,zmm1,[rbp-0x170]
229: vaddpd        zmm1,zmm2,[rbp-0x70]
233: vmovapd       [rbp-0x70],zmm1
23d: vmovapd       [rbp-0x170],zmm0
247: cmp           rdi,rax
24a: jne           130

Listing 33: Assembly of critical o-loop produced by the GNU compiler.

On our test system, this sequence of instructions yields 36.36 GFLOP/s in single threaded mode and 1375.06 GFLOP/s when running with 96 threads.

G++ also uses very few zmm registers, preferring to write out running sums to memory. It also maintains separate running sums for each of the unrolled loop sections necessitating a large number of memory read & write operations. For example, lines 15d & 169 compute the updated running sums for the numerator and denominator of Equation (9) for the first unrolled iteration and store the results in the zmm6 & zmm5 registers. Lines 18f & 199 compute the updated running sums for the numerator and denominator of Equation (9) for the second unrolled iteration. However, instead of leaving these running sums in the registers that they are computed in, G++ issues instructions that write the contents of these registers to memory on lines 1a3 & 1b7. The same pattern is observed in the third and fourth un-peeled loop iterations for a total of 22 memory accesses per v-loop iteration (16 read accesses and 6 write accesses).

The Intel C++ compiler & AOCC compiled codes perform 10 memory reads per iteration of the v-loop as opposed to the 16 reads and 6 writes performed by the G++ produced code. Each read/write operation has a latency of 4 cycles (L1 cache), 12 cycles (L2 cache), and 44 cycles (L3 cache). Arithmetic instructions such as vaddpd, vfmadd213pd, etc. have latencies of 4 to 6 cycles and throughputs of 0.5 cycles (see this manual). Since the read-write operations performed in Listing 33 are heavily predicated on the arithmetic instructions due to the low register usage, the latency of the read-write operation is more relevant than the throughput. Therefore, even a few extra read-write operations add significantly to the total number of CPU cycles required to perform a single iteration of the v-loop.

We believe that the extra read-write instructions used by the code compiled with G++ are ultimately responsible for the observed performance difference.

C.5. Clang

We compile the code using the compile line in Listing 34.

clang++ -o critical.o -c critical.cpp -D__ALGORITHM__=OBLKIO_OPT -D__AUTO__
        -O3 -std=c++14 -m64
        -ffast-math -fassociative-math -mfma -mavx2 -ffp-contract=fast
        -fopenmp=libomp
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize
        -fsave-optimization-record
        -gline-tables-only -gcolumn-info
        -mllvm -polly
        -mllvm -polly-vectorizer=stripmine
        -march=skylake-avx512

Listing 34: Compile line for compiling the structure function critical.cpp source file with Clang.

Listing 35 shows the assembly instructions generated by Clang for the time consuming inner v-loop using the Intel syntax. Only 4 out of the 32 available zmm registers are used.

290: vbroadcastsd  zmm1,[rsi+r13*8]
297: vbroadcastsd  zmm0,[rdi+r13*8]
29e: test          r12b,r12b
2a1: vmulpd        zmm2,zmm1,[r15+r13*8-0xc0]
2a9: vmovupd       zmm3,[rdx+r13*8-0xc0]
2b1: vsubpd        zmm3,zmm3,zmm0
2b7: vmulpd        zmm3,zmm3,zmm3
2bd: vfmadd213pd   zmm3,zmm2,[rsp+0x160]
2c8: vmovupd       [rsp+0x160],zmm3
2d3: vaddpd        zmm2,zmm2,[rsp+0x60]
2de: vmovupd       [rsp+0x60],zmm2
2e9: vmulpd        zmm2,zmm1,[r15+r13*8-0x80]
2f1: vmovupd       zmm3,[rdx+r13*8-0x80]
2f9: vsubpd        zmm3,zmm3,zmm0
2ff: vmulpd        zmm3,zmm3,zmm3
305: vfmadd213pd   zmm3,zmm2,[rsp+0x1a0]
310: vmovupd       [rsp+0x1a0],zmm3
31b: vaddpd        zmm2,zmm2,[rsp+0xa0]
326: vmovupd       [rsp+0xa0],zmm2
331: vmulpd        zmm2,zmm1,[r15+r13*8-0x40]
339: vmovupd       zmm3,[rdx+r13*8-0x40]
341: vsubpd        zmm3,zmm3,zmm0
347: vmulpd        zmm3,zmm3,zmm3
34d: vfmadd213pd   zmm3,zmm2,[rsp+0x1e0]
358: vmovupd       [rsp+0x1e0],zmm3
363: vaddpd        zmm2,zmm2,[rsp+0xe0]
36e: vmovupd       [rsp+0xe0],zmm2
379: vmulpd        zmm1,zmm1,[r15+r13*8]
380: vmovupd       zmm2,[rdx+r13*8]
387: vsubpd        zmm0,zmm2,zmm0
38d: vmulpd        zmm0,zmm0,zmm0
393: vfmadd213pd   zmm0,zmm1,[rsp+0x220]
39e: vmovupd       [rsp+0x220],zmm0
3a9: vaddpd        zmm0,zmm1,[rsp+0x120]
3b4: vmovupd       [rsp+0x120],zmm0
3bf: add           r13,0x1
3c3: cmp           r13,rax
3c6: jl            290

Listing 35: Assembly of critical o-loop produced by the LLVM compiler.

On our test system, this sequence of instructions yields 23.35 GFLOP/s in single threaded mode and 837.42 GFLOP/s when running with 96 threads.

Clang produces simple and easy to follow code. At the top of the loop, the values of M[i] & A[i] are loaded into the zmm1 & zmm0 registers at lines 290 & 297.
vmulpd
vmovupd
vsubpd
vmulpd
vfmadd213pd
vmovupd
vaddpd
vmovupd
executes one unrolled loop iteration to update the numerator & denominator of Equation (9).

Each sequence makes 26 memory accesses consisting of 18 reads and 8 writes to memory – four greater than in the case of the code compiled with G++ and 16 greater than in the case of the code compiled with Intel C++ compiler & AOCC. We believe that these extra memory operations are responsible for the observed performance difference between the codes generated by the different compilers.

C.6. Zapcc

We compile the code using the compile line in Listing 36.

zapcc++ -o critical.o -c critical.cpp -D__ALGORITHM__=OBLKIO_OPT -D__AUTO__
        -O3 -std=c++14 -m64 
        -ffast-math -fassociative-math -mfma -mavx2 -ffp-contract=fast
        -fopenmp=libomp
        -Rpass=loop-vectorize -Rpass-missed=loop-vectorize 
        -Rpass-analysis=loop-vectorize
        -fsave-optimization-record
        -gline-tables-only -gcolumn-info
        -march=skylake-avx512

Listing 36: Compile line for compiling the structure function critical.cpp source file with Zapcc.

Listing 37 shows the assembly instructions generated by Clang for the time consuming inner v-loop using the Intel syntax. Only 4 out of the 32 available zmm registers are used.

290: vbroadcastsd  zmm1,[r14+r13*8]
297: vbroadcastsd  zmm0,[rbx+r13*8]
29e: test          r12b,r12b
2a1: je            380
2a7: vmulpd        zmm2,zmm1,[r15+r13*8-0xc0]
2af: vmovupd       zmm3,[rdx+r13*8-0xc0]
2b7: vsubpd        zmm3,zmm3,zmm0
2bd: vmulpd        zmm3,zmm3,zmm3
2c3: vfmadd213pd   zmm3,zmm2,[rsp+0x160]
2ce: vmovupd       [rsp+0x160],zmm3
2d9: vaddpd        zmm2,zmm2,[rsp+0x60]
2e4: vmovupd       [rsp+0x60],zmm2
2ef: vmulpd        zmm2,zmm1,[r15+r13*8-0x80]
2f7: vmovupd       zmm3,[rdx+r13*8-0x80]
2ff: vsubpd        zmm3,zmm3,zmm0
305: vmulpd        zmm3,zmm3,zmm3
30b: vfmadd213pd   zmm3,zmm2,[rsp+0x1a0]
316: vmovupd       [rsp+0x1a0],zmm3
321: vaddpd        zmm2,zmm2,[rsp+0xa0]
32c: vmovupd       [rsp+0xa0],zmm2
337: vmulpd        zmm2,zmm1,[r15+r13*8-0x40]
33f: vmovupd       zmm3,[rdx+r13*8-0x40]
347: vsubpd        zmm3,zmm3,zmm0
34d: vmulpd        zmm3,zmm3,zmm3
353: vfmadd213pd   zmm3,zmm2,[rsp+0x1e0]
35e: vmovupd       [rsp+0x1e0],zmm3
369: vaddpd        zmm2,zmm2,[rsp+0xe0]
374: jmp           44d
380: vmulpd        zmm2,zmm1,[r15+r13*8-0xc0]
388: vmovupd       zmm3,[rdx+r13*8-0xc0]
390: vsubpd        zmm3,zmm3,zmm0
396: vmulpd        zmm3,zmm3,zmm3
39c: vfmadd213pd   zmm3,zmm2,[rsp+0x160]
3a7: vmovupd       [rsp+0x160],zmm3
3b2: vaddpd        zmm2,zmm2,[rsp+0x60]
3bd: vmovupd       [rsp+0x60],zmm2
3c8: vmulpd        zmm2,zmm1,[r15+r13*8-0x80]
3d0: vmovupd       zmm3,[rdx+r13*8-0x80]
3d8: vsubpd        zmm3,zmm3,zmm0
3de: vmulpd        zmm3,zmm3,zmm3
3e4: vfmadd213pd   zmm3,zmm2,[rsp+0x1a0]
3ef: vmovupd       [rsp+0x1a0],zmm3
3fa: vaddpd        zmm2,zmm2,[rsp+0xa0]
405: vmovupd       [rsp+0xa0],zmm2
410: vmulpd        zmm2,zmm1,[r15+r13*8-0x40]
418: vmovupd       zmm3,[rdx+r13*8-0x40]
420: vsubpd        zmm3,zmm3,zmm0
426: vmulpd        zmm3,zmm3,zmm3
42c: vfmadd213pd   zmm3,zmm2,[rsp+0x1e0]
437: vaddpd        zmm2,zmm2,[rsp+0xe0]
442: vmovupd       [rsp+0x1e0],zmm3
44d: vmovupd       [rsp+0xe0],zmm2
458: vmulpd        zmm1,zmm1,[r15+r13*8]
45f: vmovupd       zmm2,[rdx+r13*8]
466: vsubpd        zmm0,zmm2,zmm0
46c: vmulpd        zmm0,zmm0,zmm0
472: vfmadd213pd   zmm0,zmm1,[rsp+0x220]
47d: vmovupd       [rsp+0x220],zmm0
488: vaddpd        zmm0,zmm1,[rsp+0x120]
493: vmovupd       [rsp+0x120],zmm0
49e: add           r13,0x1
4a2: cmp           r13,rax
4a5: jl            290

Listing 37: Assembly of critical v-loop produced by the ZAPCC compiler.

On our test system, this sequence of instructions yields 23.40 GFLOP/s in single threaded mode and 840.57 GFLOP/s when running with 96 threads.

Although this sequence of instructions appears to be longer and more involved than that produced by Clang, a closer look shows that the instructions between lines 2a7 and 369 are repeated in lines 380 through 442. The test & je instruction pair on lines 29e & 2a1 jump execution to line 380 if the r12b register contains 0, bypassing the instructions between lines 2a7 and 369. On the other hand, if the r12b register does not contain 0, the instructions between 2a7 and 369 are executed and control jumps on line 374 to line 44d bypassing the repeated block between lines 380 and 442. While it is impossible to tell which branch is used more often without knowing what the contents of the r12b register are, it is likely that one of the branches is taken very infrequently.

Since both blocks contain the exact same instructions, it is not clear what the purpose of the complicated jumps is. A clue may be found in the Clang listings (Listing 35). Notice that both Listings 35 and 37 contain the same instructions, including the test instruction (line 29e in both listings). However, while the Zapcc produced listings follow the test with a je, the Clang produced listings omit the jump instruction along with one of the two blocks of identical code.

We hypothesize that Zapcc skips some of the steps taken by Clang to remove dead code, etc. This may explain how Zapcc manages to produce equally optimized code but with a much shorter compile time than Clang.

C.7. PGC++

We compile the code using the compile line in Listing 38.

pgc++ -o critical.o -c critical.cpp -D__ALGORITHM__=OBLKIO_OPT -D__AUTO__
      -O3 -tp=haswell -fast -O4 -fma
      -Msmart -Mfma -Mcache_align
      -Mipa=all -Mmovnt -mp -Mquad
      -Msafeptr=all -Minfo=all
      -Mnoprefetch

Listing 38: Compile line for compiling the structure function critical.cpp source file with PGC++.

Listing 39 shows the assembly instructions generated by PGC++ for the time consuming inner v-loop using the Intel syntax. Only 6 out of the 16 available ymm registers are used.

680: mov           r15,[rsp+0x3c8]
688: vmovupd       ymm2,[r15+rax*1]
68e: vsubpd        ymm3,ymm2,ymm0
692: mov           r15,[rsp+0x3c0]
69a: vmovupd       ymm2,[r15+rax*1]
6a0: vmulpd        ymm4,ymm2,ymm1
6a4: vmulpd        ymm5,ymm4,ymm3
6a8: mov           r15,[rsp+0x3b8]
6b0: vmovupd       ymm2,[r15+rax*1]
6b6: vfmadd231pd   ymm2,ymm5,ymm3
6bb: vmovupd       [r15+rax*1],ymm2
6c1: mov           r15,[rsp+0x3b0]
6c9: vmovupd       ymm2,[r15+rax*1]
6cf: vaddpd        ymm3,ymm2,ymm4
6d3: vmovupd       [r15+rax*1],ymm3
6d9: vmovupd       ymm2,[r13+rax*1+0x0]
6e0: mov           r15,[rsp+0x3a8]
6e8: vsubpd        ymm3,ymm2,ymm0
6ec: vmovupd       ymm2,[r15+rax*1]
6f2: vmulpd        ymm4,ymm2,ymm1
6f6: vmulpd        ymm5,ymm4,ymm3
6fa: vmovupd       ymm2,[r14+rax*1]
700: vfmadd231pd   ymm2,ymm5,ymm3
705: vmovupd       [r14+rax*1],ymm2
70b: vmovupd       ymm3,[r12+rax*1]
711: vaddpd        ymm2,ymm3,ymm4
715: vmovupd       [r12+rax*1],ymm2
71b: vmovupd       ymm3,[r10+rax*1]
721: vmovupd       ymm4,[rbx+rax*1]
726: vsubpd        ymm2,ymm3,ymm0
72a: vmulpd        ymm3,ymm4,ymm1
72e: vmulpd        ymm5,ymm3,ymm2
732: vmovupd       ymm4,[r11+rax*1]
738: vfmadd231pd   ymm4,ymm5,ymm2
73d: vmovupd       [r11+rax*1],ymm4
743: vmovupd       ymm2,[r9+rax*1]
749: vaddpd        ymm4,ymm2,ymm3
74d: vmovupd       [r9+rax*1],ymm4
753: vmovupd       ymm2,[rsi+rax*1]
758: vmovupd       ymm4,[r8+rax*1]
75e: vsubpd        ymm3,ymm2,ymm0
762: vmulpd        ymm2,ymm1,ymm4
766: vmulpd        ymm5,ymm2,ymm3
76a: vmovupd       ymm4,[rdi+rax*1]
76f: vfmadd231pd   ymm4,ymm5,ymm3
774: vmovupd       [rdi+rax*1],ymm4
779: vmovupd       ymm3,[rdx+rax*1]
77e: vaddpd        ymm4,ymm3,ymm2
782: vmovupd       [rdx+rax*1],ymm4
787: add           rax,0x20
78b: cmp           rax,rcx
78e: jb            680

Listing 39: Assembly of critical v-loop produced by the PGI compiler.

On our test system, this sequence of instructions yields 12.82 GFLOP/s in single threaded mode.

PGC++ does not support AVX-512 instruction generation as of the 17.4 Community Edition and 17.9 Professional Edition. Hence we instruct the compiler to target the Haswell microarchitecture.The resulting assembly contains AVX2 instructions and uses 256-bit wide ymm registers as opposed to the 512-bit wide zmm registers.

There are a total of 16 memory read instructions and 8 memory write instructions for a total of 24 memory operations per iteration of the v-loop.

We believe that the number of memory operations combined with the usage of AVX2 instructions as opposed to AVX-512 instructions explains the relatively poor performance observed with the PGC++ generated code.

C.8. Takeaway

Hand tuning code for optimal performance always yields superior performance from every compiler. However, the absolute performance achieved by the different compilers can still be very different. Disregarding the PGC++ results because they are not generated using AVX-512 instructions, in this computational kernel we see a performance difference of 2.5x between the best and worst performing compilers (Intel C++ compiler v/s Clang).

Appendix D. Compilation Speed

Our test for compilation speed sets each compiler with the goal of compiling the templated C++ linear algebra library ‘TMV’. We pick TMV because the library supports all our compilers right of the box. Furthermore, the total single threaded compile time is manageable, i.e., long enough to eliminate statistical variations in compile time for individual files but short enough to obtain results quickly.

The TMV codebase consists of approximately 370 source and header files including files for instantiating templates. TMV uses the Python-based SCons build system to manage the build process. We had to make minor modifications to the top-level SConstruct file to update a few deprecated compiler options and include paths in order to get the build system to successfully build the project with each compiler. Our changes do not substantially change the build process.

Listing 40 shows the TMV implementation of LU decomposition with partial pivoting. We have performed minor edits to the code to remove commented out code and debug sections. As is clear from the listings, the TMV codebase makes heavy use of advanced C++ techniques and is representative of modern C++ codebases.

It should come as no surprise that the Zapcc compiler is the fastest compiler. The LLVM infrastructure is designed to support just-in-time (JIT) compilation for languages such as Julia, and Crystal. JIT compiled languages rely on compiler speed to obfuscate the comp;ile process. LLVM-based compilers are amongst the fastest compilers in the test. Zapcc was designed to provide a speed advantage over Clang.

The slowest compiler in the test is the PGI compiler. At 2750 seconds of compile time, PGC++ takes 5.4x longer to compile our test case than Zapcc. PGI is working on an LLVM-based version of the PGI compiler that should be significantly faster.

  template  
  static void NonBlockLUDecompose(MatrixView A, ptrdiff_t* P) {
      TMVAssert(A.ct()==NonConj);
      TMVAssert(A.iscm());
      typedef TMV_RealType(T) RT;
      const ptrdiff_t N = A.rowsize();
      const ptrdiff_t M = A.colsize();
      const ptrdiff_t R = TMV_MIN(N,M);
      const T* Ujj = A.cptr();
      const ptrdiff_t Ads = A.stepj()+1;
      ptrdiff_t* Pj = P;
      for (ptrdiff_t j=0; j<R; ++j,Ujj+=Ads,++Pj) { if (j > 0) {
              // Solve for U(0:j,j))
              A.col(j,0,j) /= A.subMatrix(0,j,0,j).lowerTri(UnitDiag);
              // Solve for v = L(j:M,j) U(j,j)
              A.col(j,j,M) -= A.subMatrix(j,M,0,j) * A.col(j,0,j);
          }
          // Find the pivot element
          ptrdiff_t ip;
          RT piv = A.col(j,j,M).maxAbsElement(&ip);
          // ip is relative to j index, not absolute.
          // Check for underflow:
          if (TMV_Underflow(piv)) {
              *Pj = j;
              A.col(j,j,M).setZero();
              continue;
          }
          // Swap the pivot row with j if necessary
          if (ip != 0) {
              ip += j;
              TMVAssert(ip < A.colsize());
              TMVAssert(j < A.colsize()); A.swapRows(ip,j); // This does both Lkb and A' *Pj = ip; } else *Pj = j; // Solve for L(j+1:M,j) // If Ujj is 0, then all of the L's are 0. // ie. Ujj Lij = 0 for all i>j
          // Any value for Lij is valid, so leave them 0.
          if (*Ujj != T(0)) A.col(j,j+1,M) /= *Ujj;
      }
      if (N > M) {
          // Solve for U(0:M,M:N))
          A.colRange(M,N) /= A.colRange(0,M).lowerTri(UnitDiag);
      }
  }

Listing 40: Sample TMV code for non-block LU decomposition with partial pivoting.

Share this:

Table of Contents

1. The Importance of a Good Compiler

2. Testing Methodology

2.1. Meet the Compilers

2.2. Target Architecture

2.3. Computational Kernels

2.4. Compilation Time

2.5. Test Details

2.6. Test Platform

2.7. Code Analysis

3. Results

3.1. Performance of Compiled Code

3.2. Compilation Speed

4. Summary

Appendix A. LU Decomposition

A.1. What is pivotless LU Decomposition and How does it work?

A.2. Intel C++ compiler

A.3. G++

A.4. PGC++

A.5. AOCC

A.6. Clang

A.7. Zapcc

A.8. Takeaway

Appendix B. Jacobi Solver

B.1. What does a Jacobi Solver solve?

B.2. Intel C++ compiler

B.3. G++

B.4. AOCC

B.5. Clang

B.6. Zapcc

B.7. PGC++

B.8. Takeaway

Appendix C. Structure Function

C.1. What is the Structure Function?

C.2. Intel C++ compiler

C.3. AOCC

C.4. G++

C.5. Clang

C.6. Zapcc

C.7. PGC++

C.8. Takeaway

Appendix D. Compilation Speed

Share this: