Capabilities of Intel® AVX-512 in Intel® Xeon® Scalable Processors (Skylake)

This paper reviews the Intel® Advanced Vector Extensions 512 (Intel® AVX-512) instruction set and answers two critical questions:
- How do Intel® Xeon® Scalable processors based on the Skylake architecture (2017) compare to their predecessors based on Broadwell due to AVX-512?
- How are Intel Xeon processors based on Skylake different from their alternative, Intel® Xeon Phi™ processors with the Knights Landing architecture, which also feature AVX-512?
We address these questions from the programmer’s perspective by demonstrating C language code of microkernels benefitting from AVX-512. For each example, we dig deeper and analyze the compilation practices, resultant assembly, and optimization reports.
In addition to code studies, the paper contains performance measurements for a synthetic benchmark with guidelines on estimating peak performance. In conclusion, we outline the workloads and application domains that can benefit from the new features of AVX-512 instructions.
![]() Colfax-SKL-AVX512-Guide.pdf (524 KB)
Colfax-SKL-AVX512-Guide.pdf (524 KB)
Table of Contents
- 1. Intel Advanced Vector Extensions 512
- 1.1. Instruction Sets in Intel architecture
- 1.2. AVX-512 Modules
- 1.3. Automatic Vectorization
- 2. Skylake and Broadwell
- 2.1. AVX-512: ZMM Registers
- 2.2. Clock Frequency and Peak Performance
- 2.3. AVX-512CD: Conflict Detection
- 2.4. AVX-512F: Masking
- 2.5. AVX-512F: Compress/Expand
- 2.6. AVX-512F: New Shuffle Instructions
- 2.7. AVX-512F: Gather/Scatter
- 2.8. AVX-512F: Embedded Broadcasting
- 2.9. AVX-512F: Ternary Logic
- 2.10. AVX-512F: Embedded Rounding
- 3. Skylake and Knights Landing
- 3.1. AVX-512ER: Exponential, Reciprocal
- 3.2. AVX-512PF: Prefetch for Gather/Scatter
- 3.3. AVX-512DQ: Double and Quad Words
- 3.4. AVX-512BW: Byte and Word Support
- 3.5. AVX-512VL: Vector Length Orthogonality
- 4. Applicability of AVX-512
1. Intel Advanced Vector Extensions 512
1.1. Instruction Sets in Intel architecture
Vector instructions are an essential functionality of modern processors. These instructions are one of the forms of SIMD (Single Instruction Multiple Data) parallelism. Vector instructions enable faster computing in cases where a single stream of instructions inside a process or thread may be applied to multiple data elements. For example, the addition (multiplication) of two arrays element by element can be performed with vector instructions, which add (multiply) several elements concurrently. Other instructions in modern vector instruction sets include fused multiply-add (FMA), some transcendental functions, division and reciprocal calculation. Some instruction sets support vector lane masking, permutation, and shuffling. Depending on the data type and CPU architecture, modern Intel processors can operate on vectors of 2 to 16 floating-point numbers or 2 to 64 integers.
Intel architecture processors support legacy as well as modern instruction sets, from 64-bit Multimedia Extensions (MMX) to the new 512-bit instructions AVX-512. Newer instruction sets generally provide a greater variety of operations and data types and also support larger vectors. As new Intel architecture processors are released, they support newer instruction sets, usually maintaining backward compatibility with the older ones. The figure below shows the microarchitecture codenames, model families and supported instructions in enterprise-class Intel processors dating back to 2009.
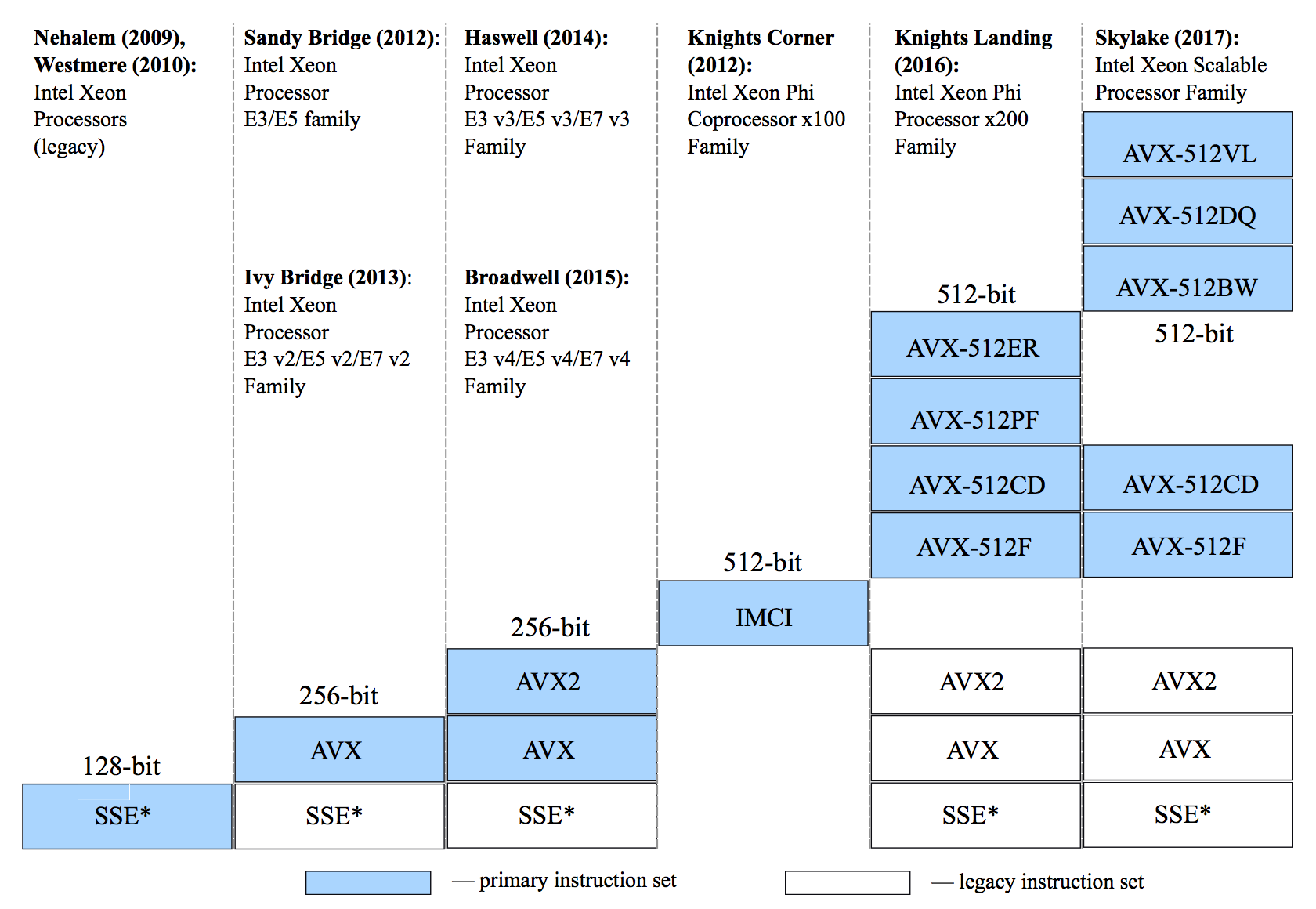
Figure 1: Instruction sets supported by different architectures.
At the time of writing (September 2017), the most recent of the widely adopted enterprise processors use vector instructions up to Intel AVX® and Intel® AVX2. Specifically, these instructions are the foundation of the Intel® Xeon® E5 v4 processor family (formerly Broadwell) introduced in 2015. AVX and AVX2 had been the most advanced of Intel instruction sets until the introduction of Intel® Advanced Vector Extensions 512 (Intel® AVX-512 or just AVX-512 in subsequent discussion). AVX-512 as first used in Intel® Xeon Phi™ processor family x200 (formerly Knights Landing) launched in 2016. Later, in 2017, AVX-512 was used in Intel® Xeon® processor Scalable family (formerly Skylake).
The most notable new feature of AVX-512 compared to AVX/AVX2 is the 512-bit vector register width, which is twice the size of the AVX/AVX2 registers. However, AVX-512 is more than just a promotion of the vector register width from 256 to 512 bits. It adds capabilities that did not exist in AVX/AVX2 and earlier instruction sets, such as high-accuracy transcendental functions, histogram support, byte, word, double word and quadword scalar data types, masking, and others.
To developers and maintainers of computational codes, the introduction of AVX-512 is a call for action. AVX-512 instructions offer significant speedup when used in applications. However, this speedup is not automatic, and the software developer is responsible for enabling vector processing in computational codes. In this paper, we study the developer’s perspective on the innovations brought about by AVX-512.
1.2. AVX-512 Modules
Skylake and Knights Landing implement different flavors of AVX-512. The Knights Landing architecture uses modules AVX-512F, -CD, -ER and -PF. Two of these modules, AVX-512F and -CD are also found in the Skylake architecture, which additionally features AVX-512DQ, -BW and -VL. The table below shows AVX-512 modules found in Skylake (SKL) and Knights Landing (KNL) architectures and lists the main functionality of each module.
| Module | Functionality | SKL | KNL |
|---|---|---|---|
| AVX-512F | The fundamental instruction set, it expands most of AVX functions to support 512-bit registers and adds masking, embedded broadcasting, embedded rounding and exception control. | ✓ | ✓ |
| AVX-512CD | Conflict Detection instruction set allows vectorization of loops with vector dependency due to writing conflicts | ✓ | ✓ |
| AVX-512BW | Byte and Word support instruction set: 8-bit and 16-bit integer operations, processing up to 64 8-bit elements or 32 16-bit integer elements per vector | ✓ | |
| AVX-512DQ | Double and Quad word instruction set, supports new instructions for double-word (32-bit) and quadword (64-bit) integer and floating-point elements | ✓ | |
| AVX-512VL | Vector Length extensions: support for vector lengths smaller than 512 bits | ✓ | |
| AVX-512PF | Data prefetching for gather and scatter instructions | ✓ | |
| AVX-512ER | Exponential and Reciprocal instruction set for high-accuracy base-2 exponential functions, reciprocals, and reciprocal square root | ✓ |
Table 1: AVX-512 modules, functionality, and architectures supporting each module.
In anticipation of future Intel architectures, it is important to mention that not all AVX-512 modules are required to be supported by all architectures implementing them. AVX-512F, the Fundamental extensions, is the only module required to be supported by all future architectures implementing AVX-512.
1.3. Automatic Vectorization
There are two essential ways to take advantage of wide vector registers and vectorization benefits:
- explicit vectorization using assembly and intrinsic functions and
- automatic vectorization of loops by the compiler.
Although explicit vectorization is more controllable, it lacks portability. For instance, code using AVX-512 assembly or intrinsics will not work on an older processor that only supports instruction sets up to AVX2 (e.g., Broadwell architecture, BDW). Conversely, code using explicit AVX/AVX2 instructions will work on a Skylake or Knights Landing architecture, but in legacy mode, where it uses half the register width and incomplete functionality. In contrast, automatic vectorization is portable. If the compiler can vectorize a code for an older instruction set, then usually it can also vectorize it for newer instructions. Therefore, only a recompilation is needed to produce an executable for a new processor architecture.
The table below shows the compiler arguments required for automatic vectorization with AVX-512 using Intel C/C++/FORTRAN compilers 17/18 and the corresponding arguments for GNU and LLVM compilers.
| Compiler | Intel compilers 17.x | Intel compilers 18.x | GNU and LLVM |
|---|---|---|---|
| Cross-platform | -xCommon-AVX512 | -xCommon-AVX512 | -mfma -mavx512f -mavx512cd |
| SKL processors | -xCore-AVX512 | -xCore-AVX512 -qopt-zmm-usage=high | -march=skylake-avx512 |
| KNL processors | -xMIC-AVX512 | -xMIC-AVX512 | -march=knl |
Table 2: AVX-512 compilation flags for Intel C/C++, FORTRAN, GNU and LLVM compilers.
In Intel compilers, automatic vectorization is enabled at the default optimization level -O2, so no additional arguments are needed. In GCC, to enable automatic vectorization, use the additional argument -O3. Additionally, to vectorize transcendental functions with GCC, -ffast-math may be needed.
The listing below is an example of code that may be automatically vectorized by the compiler.
void VectorAddition(double * restrict A, double * restrict B) {
int i;
for(i = 0; i < 10000; i++)
A[i]+=B[i];
}Listing 1: Automatic vectorization example, auto_vec.c.
When the loop count (10000 in our case) is greater than the vector width, the compiler can combine several scalar iterations of the loop into a single vector iteration and run the loop over the vector iterations. With AVX-512, the vector width for double precision floating-point elements is 8, for single precision elements it is 16. When the loop count is not a multiple of the vector width, a remainder loop will be executed. Automatic vectorization does not require that the loop count is known at compilation time (i.e., we could use a variable n instead of the constant 10000). However, if it is known at compilation time, the compiler may choose a more efficient vectorization strategy.
The listing below shows how to compile the example code to produce an auto-vectorized object file (first command), assembly listing (second command), and optimization report (third command). Throughout the paper we use Intel compiler 17.0.2.174 and the corresponding arguments mentioned above.
icc -xCORE-AVX512 -c auto_vec.c
icc -xCORE-AVX512 -S auto_vec.c
icc -xCORE-AVX512 -c auto_vec.c -qopt-report=5 Listing 2: Compilation commands to produce an object file, an assembly listing, and an optimization report.
The first command line in the above listing will produce an object file auto_vec.o that can be linked to an executable and run on the target architecture.
The second command will produce an assembly listing in the file auto_vec.s instead of machine code. The snippet in the listing below shows the loop part of this assembly listing. You can identify the loop pattern by matching the label B1.8 to the combination of counter increment addq, loop termination condition check cmpq and conditional jump jb back to B1.8.
user@node% cat auto_vec.s
...
..B1.8: # Preds ..B1.8 ..B1.7
vmovups (%rdi,%r8,8), %zmm0 #4.5
vmovups 64(%rdi,%r8,8), %zmm1 #4.5
vmovups 128(%rdi,%r8,8), %zmm4 #4.5
vmovups 192(%rdi,%r8,8), %zmm5 #4.5
vaddpd (%rsi,%r8,8), %zmm0, %zmm2 #4.5
vaddpd 64(%rsi,%r8,8), %zmm1, %zmm3 #4.5
vaddpd 128(%rsi,%r8,8), %zmm4, %zmm6 #4.5
vaddpd 192(%rsi,%r8,8), %zmm5, %zmm7 #4.5
vmovupd %zmm2, (%rdi,%r8,8) #4.5
vmovupd %zmm3, 64(%rdi,%r8,8) #4.5
vmovupd %zmm6, 128(%rdi,%r8,8) #4.5
vmovupd %zmm7, 192(%rdi,%r8,8) #4.5
addq $32, %r8 #3.3
cmpq %rdx, %r8 #3.3
jb ..B1.8 # Prob 99% #3.3
... Listing 3: Lines from the auto-vectorized assembly code.
Vectorization is apparent in this code because the instruction vmovups loads the data from memory into the vector register, and vaddpd adds one vector to another. Here the prefix v- indicates the vector instruction, add is the name of the instruction, and the suffix -pd stands for “packed double”, i.e., the operation applies to a vector of double precision floating-point numbers. Other suffixes you may see include: -ps (“packed single”), -epi64/-epi32/-epi16/-epi8 for vectors of signed 64-, 32-, 16- or 8-bit integers; -epu64/-epu32/-epu16/-epu8 for vectors of unsigned integers; and suffixes indicating the absence of vectorization: -sd (“scalar double”) and -ss (“scalar single”). The names of the registers beginning with ZMM indicate 512-bit vectors of AVX-512. For other instruction sets, you may see 256-bit YMM registers (AVX/AVX2) or 128-bit XMM registers (SSE*).
In addition to studying the assembly, you can diagnose vectorization using the optimization report. To do that, compile the file with the argument -opt-report=n, where n is the desired verbosity level from 1 to 5. In our case, the command produces an optimization report file auto_vec.optrpt, in which you will find the remarks shown in the listing below.
user@node% cat auto_vec.optrpt
... LOOP BEGIN at auto_vec.c(3,3)
remark #15389: vectorization support: reference A[i] has unaligned access [ auto_vec.c(4,5) ]
remark #15389: vectorization support: reference A[i] has unaligned access [ auto_vec.c(4,5) ]
remark #15389: vectorization support: reference B[i] has unaligned access [ auto_vec.c(4,11) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15305: vectorization support: vector length 8
remark #15309: vectorization support: normalized vectorization overhead 1.167
remark #15301: PEEL LOOP WAS VECTORIZED
remark #25015: Estimate of max trip count of loop=1
LOOP END
LOOP BEGIN at auto_vec.c(3,3)
remark #15388: vectorization support: reference A[i] has aligned access [ auto_vec.c(4,5) ]
remark #15388: vectorization support: reference A[i] has aligned access [ auto_vec.c(4,5) ]
remark #15389: vectorization support: reference B[i] has unaligned access [ auto_vec.c(4,11) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15305: vectorization support: vector length 16
remark #15399: vectorization support: unroll factor set to 2
remark #15309: vectorization support: normalized vectorization overhead 0.591
remark #15300: LOOP WAS VECTORIZED
remark #15442: entire loop may be executed in remainder
remark #15448: unmasked aligned unit stride loads: 1
remark #15449: unmasked aligned unit stride stores: 1
remark #15450: unmasked unaligned unit stride loads: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 8
remark #15477: vector cost: 0.680
remark #15478: estimated potential speedup: 11.550
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=312
LOOP END
LOOP BEGIN at auto_vec.c(3,3)
remark #15389: vectorization support: reference A[i] has unaligned access [ auto_vec.c(4,5) ]
remark #15389: vectorization support: reference A[i] has unaligned access [ auto_vec.c(4,5) ]
remark #15389: vectorization support: reference B[i] has unaligned access [ auto_vec.c(4,11) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15305: vectorization support: vector length 8
remark #15309: vectorization support: normalized vectorization overhead 1.167
remark #15301: REMAINDER LOOP WAS VECTORIZED
LOOP END
...Listing 4: Optimization report produced by the Intel C compiler.
In this particular example we see that the compiler produced three parts of the loop:
- A peel loop designed to process a few elements at the start of the loop to reach an aligned boundary in memory. This loop is taken only if the beginning of A is not on a 64-byte aligned boundary (i.e., memory address of A[0] is not a multiple of 64 bytes).
- The main loop that processes the bulk of the iterations, starting with the aligned address to which the peel loop has progressed.
- The remainder loop that processes a few elements at the end of the loop in case the number of loop iterations minus the peel size is not a multiple of the vector length (or the vector length multiplied by the unroll factor).
In codes that have long loops or short loops with aligned data, the peel loop and the remainder loop do not take a significant fraction of the processing time. Therefore, for our discussions in this paper, we will be only interested in the main loop.
When we produce the assembly with -S, we find it useful to use an additional compiler argument, -qopt-report-embed, which inserts remarks about vectorization into the assembly. In particular, it helps us to distinguish between the code for the peel loop, the main loop, and the remainder loop. You can see how they look in the listing below. We do not show these remarks in assembly listings in the rest of this paper, but we used them in the writing process to identify the main loop body.
user@node% icc -xCORE-AVX512 -S auto_vec.c -qopt-report-embed
user@node% cat auto_vec.s
..L3:
# optimization report
# LOOP WAS VECTORIZED
# PEELED LOOP FOR VECTORIZATION
# MASKED VECTORIZATION
# VECTORIZATION HAS UNALIGNED MEMORY REFERENCES
# VECTORIZATION SPEEDUP COEFFECIENT 1.641602
# VECTOR TRIP COUNT IS ESTIMATED CONSTANT
# VECTOR LENGTH 8
# NORMALIZED VECTORIZATION OVERHEAD 1.125000
# MAIN VECTOR TYPE: 64-bits floating point
vpcmpud $1, %ymm0, %ymm1, %k1 #3.3
addq $8, %rcx #3.3
vpaddd %ymm2, %ymm1, %ymm1 #3.3
vmovupd (%rdx,%rdi), %zmm3{%k1}{z} #4.5
...
..L4:
# optimization report
# LOOP WAS UNROLLED BY 2
# LOOP WAS VECTORIZED
# VECTORIZATION HAS UNALIGNED MEMORY REFERENCES
# VECTORIZATION SPEEDUP COEFFECIENT 11.562500
# VECTOR TRIP COUNT IS KNOWN CONSTANT
# VECTOR LENGTH 16
# NORMALIZED VECTORIZATION OVERHEAD 0.562500
# MAIN VECTOR TYPE: 64-bits floating point
vmovups (%rdi,%r8,8), %zmm0 #4.5
vmovups 64(%rdi,%r8,8), %zmm1 #4.5
vmovups 128(%rdi,%r8,8), %zmm4 #4.5
...
..L5:
# optimization report
# LOOP WAS VECTORIZED
# REMAINDER LOOP FOR VECTORIZATION
# MASKED VECTORIZATION
# VECTORIZATION HAS UNALIGNED MEMORY REFERENCES
# VECTORIZATION SPEEDUP COEFFECIENT 3.550781
# VECTOR TRIP COUNT IS ESTIMATED CONSTANT
# VECTOR LENGTH 8
# NORMALIZED VECTORIZATION OVERHEAD 1.125000
# MAIN VECTOR TYPE: 64-bits floating point
vpcmpud $1, %ymm0, %ymm1, %k1 #3.3
lea (%rax,%rcx), %r8d #4.5
vpaddd %ymm2, %ymm1, %ymm1 #3.3
movslq %r8d, %r8 #4.5
...Listing 5: Remarks in the assembly listing produced by the Intel compiler with -qopt-report-embed.
With the GNU C compiler, the equivalent compilation commands are shown in the listing below.
gcc -O3 -march=skylake-avx512 -c auto_vec.c
gcc -O3 -march=skylake-avx512 -S auto_vec.c
gcc -O3 -march=skylake-avx5122 -c auto_vec.c -fopt-info-vecListing 6: Compilation commands for GCC to produce executable code and assembly listing.
The assembly produced by GCC 6.3.0 (see the listing below) also contains vectorized addition. However, you can see that GCC has decided not to unroll the loop, possibly leading to a less efficient implementation.
.L4:
vmovupd (%r8,%rax), %zmm0
vaddpd (%rcx,%rax), %zmm0, %zmm0
addl $1, %edx
vmovapd %zmm0, (%rcx,%rax)
addq $64, %rax
cmpl %r9d, %edx
jb .L4Listing 7: Assembly of vector addition produced by GCC.
The optimization report produced by GCC with -fopt-info-vec is much less informative than Intel compiler’s report, as shown in the listing below.
user@node% gcc -O3 -march=skylake-avx512 -S auto_vec.c -fopt-info-vec
auto_vec.c:3:3: note: loop vectorized
auto_vec.c:3:3: note: loop peeled for vectorization to enhance alignmentListing 8: Optimization report of GCC.
It is possible to obtain more information with -fopt-info-vec-all, or restrict the output to failed vectorization with -fopt-info-vec-missed. However, the output of GCC with these arguments in our simple case is not as informative and as easy to read as the Intel compiler’s report. Note that the previously used argument for vectorization diagnostics, -ftree-vectorizer-verbose=n, is deprecated in version 6.3.0 of GCC that we used for the materials of this paper.
Using the correct compiler arguments for automatic vectorization is only one of the instruments in the programmer’s toolbox. In some cases, the programmer must expose vectorization opportunities, adjust data containers, guide the compiler with directives, rebalance parallelism in the application, or optimize the data traffic to get vectorization working efficiently. These techniques go beyond the scope of this paper, and we can refer you to our free training programs for more details (e.g., HOW Series “Deep Dive” or HOW Series “KNL”).
2. Skylake and Broadwell
As we mentioned above, Intel Xeon processor Scalable family based on the Skylake (SKL) microarchitecture is the first Intel Xeon product line to support AVX-512. These processors succeed the Intel Xeon processor v4 family based on the Broadwell (BDW) microarchitecture, which supports instructions from MMX and SSE to AVX and AVX2.
Section 2 explains and illustrates with examples the differences in vectorization capabilities of the Skylake and Broadwell architectures.
2.1. AVX-512: ZMM Registers
Skylake cores support 512-bit registers while Broadwell cores use 256-bit vectors. Some instructions have the same throughput (sustained number of pipelined instructions processed per cycle) on SKL and BDW. For example, both BDW and SKL have a throughput for FMA of 2 instructions per cycle. These considerations may lead to the erroneous conclusion that by just changing the width of vector iterations in the code (or the names of vector registers in the assembly), we can port a code from BDW to SKL and observe a speedup by a factor of 2 (relative to clock frequency). In reality, the porting process has several complications:
- SKL cores want to consume 2x as much data per cycle as BDW cores. However, the bandwidth of SKL caches and memory is only slightly greater than on BDW. The difference between the amount of improvement in throughput and in bandwidth means that data reuse optimizations (such as loop tiling) must be adjusted before peak performance on SKL may be observed.
- The latency of fast instructions, such as FMA, is different. On BDW, FMA from AVX2 has a latency of 5 cycles, while on SKL the latency of FMA from AVX-512 is 4 cycles (on KNL, it is 6 cycles). Therefore, more FMA instructions must be pipelined on BDW than on SKL to observe the effective throughput of 2 instructions per cycle.
- The number of available registers is different. Each SKL core supports 32 vector registers, while BDW cores have 16 registers. Additional registers expand the opportunities for pipelining and data reuse in registers on SKL.
The example in the listing below shows a benchmark of the fused multiply-add (FMA) operation.
#include <stdio.h>
#include <omp.h>
const int n_trials = 1000000000; // Enough to keep cores busy for a while and observe a steady state
const int flops_per_calc = 2; // Multiply + add = 2 instructions
const int n_chained_fmas = 10; // Must be tuned for architectures here and in blocks (R) and in (E)
int main() {
#pragma omp parallel
{ } // Warm up the threads
const double t0 = omp_get_wtime(); // start timer
#pragma omp parallel
{ // Benchmark in all threads
double fa[VECTOR_WIDTH*n_chained_fmas], fb[VECTOR_WIDTH], fc[VECTOR_WIDTH];
fa[0:VECTOR_WIDTH*n_chained_fmas] = 0.0; // prototype of a memory-based array
fb[0:VECTOR_WIDTH] = 0.5; // fixed
fc[0:VECTOR_WIDTH] = 1.0; // fixed
register double *fa01 = fa + 0*VECTOR_WIDTH; // This is block (R)
register double *fa02 = fa + 1*VECTOR_WIDTH; // To tune for a specific architecture,
register double *fa03 = fa + 2*VECTOR_WIDTH; // more or fewer fa* variables
register double *fa04 = fa + 3*VECTOR_WIDTH; // must be used
register double *fa05 = fa + 4*VECTOR_WIDTH;
register double *fa06 = fa + 5*VECTOR_WIDTH;
register double *fa07 = fa + 6*VECTOR_WIDTH;
register double *fa08 = fa + 7*VECTOR_WIDTH;
register double *fa09 = fa + 8*VECTOR_WIDTH;
register double *fa10 = fa + 9*VECTOR_WIDTH;
int i, j;
#pragma nounroll // Prevents automatic unrolling by compiler to avoid skewed benchmarks
for(i = 0; i < n_trials; i++)
#pragma omp simd // Ensures that vectorization does occur
for (j = 0; j < VECTOR_WIDTH; j++) { // VECTOR_WIDTH=4 for AVX2, =8 for AVX-512
fa01[j] = fa01[j]*fb[j] + fc[j]; // This is block (E)
fa02[j] = fa02[j]*fb[j] + fc[j]; // To tune for a specific architecture,
fa03[j] = fa03[j]*fb[j] + fc[j]; // more or fewer such FMA constructs
fa04[j] = fa04[j]*fb[j] + fc[j]; // must be used
fa05[j] = fa05[j]*fb[j] + fc[j];
fa06[j] = fa06[j]*fb[j] + fc[j];
fa07[j] = fa07[j]*fb[j] + fc[j];
fa08[j] = fa08[j]*fb[j] + fc[j];
fa09[j] = fa09[j]*fb[j] + fc[j];
fa10[j] = fa10[j]*fb[j] + fc[j];
}
fa[0:VECTOR_WIDTH*n_chained_fmas] *= 2.0; // Prevent dead code elimination
}
const double t1 = omp_get_wtime();
const double gflops = 1.0e-9*(double)VECTOR_WIDTH*(double)n_trials*(double)flops_per_calc*
(double)omp_get_max_threads()*(double)n_chained_fmas;
printf("Chained FMAs=%d, vector width=%d, GFLOPs=%.1f, time=%.6f s, performance=%.1f GFLOP/s\n",
n_chained_fmas, VECTOR_WIDTH, gflops, t1 - t0, gflops/(t1 - t0));
}Listing 9: Fused multiply-add (FMA) benchmark with 10 chained FMAs.
This code is written in a way that the dataset can be contained completely in the registers. Therefore, it is a pure test of performance. The code issues several FMA instructions in a row, which are independent (do not have to wait for each other’s results). Multiple instructions are needed to populate the pipeline with sufficient amount of work, which will help to achieve the performance limited by the FMA instruction throughput, rather than latency. Therefore, n_chained_fmas must be chosen to be no less than the ratio of the FMA latency (in cycles) to its reciprocal throughput (cycles per instruction). At the same time, this value must be small enough that all of the fa* variables can be contained within the registers of one core. Correspondingly, lines must be added or removed in blocks (R) and (E).
The dependence of the optimal number of chained FMAs on the architecture means that to tune the code for Broadwell or Skylake, slightly different codes must be used for the two architectures. That is, of course, in addition to using different compilation arguments for automatic vectorization.
We can estimate the optimal range for n_chained_fmas for both architectures.
- For Broadwell, FMA has a latency of 5 cycles and reciprocal throughput of 0.5 cycle (i.e., 2 instructions per cycle), so the number of chained FMAs must be no less than 5/0.5=10. At the same time, with 16 registers per core, and two of them occupied by fb and fc, we can only use up to 16-2=14 chained FMAs. So n_chained_fmas must be between 10 and 14, inclusive.
- For Skylake, FMA has a latency of 4 cycles and reciprocal throughput of 0.5 cycle (i.e., 2 instructions per cycle), so the number of chained FMAs must be no less than 4/0.5=8. At the same time, with 32 registers per core, and two of them occupied by fb and fc, we can only use up to 32-2=30 chained FMAs. So n_chained_fmas must be between 8 and 30, inclusive, which is a much wider range than for Broadwell.
To compile the code into assembly for the respective architectures, we used the commands shown in the listing below. As you can see, we are compiling different source files: for Broadwell, fma_10.c has n_chained_fmas=10, and for Skylake, fma_08.c has n_chained_fmas=8.
icpc -qopenmp -DVECTOR_WIDTH=4 -xCORE-AVX2 -S -o fma_avx2_10.s fma_10.c
icpc -qopenmp -DVECTOR_WIDTH=8 -xCORE-AVX512 -S -o fma_avx512_08.s fma_08.cListing 10: Compilation of the fused multiply-add benchmark code for Broadwell and Skylake.
The generated assembly for Broadwell looks like in the listing below. You can see the usage of vfmadd213pd with two constant registers YMM0 and YMM7, and a set of registers YMM1 … YMM6 and YMM8 … YMM11 that serve as input as well as output. YMM are 256-bit wide AVX2 registers, each containing four double precision numbers.
..B1.24: # Preds ..B1.24 ..B1.23
# Execution count [1.00e+06]
incl %eax #35.5
vfmadd213pd %ymm0, %ymm7, %ymm11 #38.35
vfmadd213pd %ymm0, %ymm7, %ymm10 #39.35
vfmadd213pd %ymm0, %ymm7, %ymm9 #40.35
vfmadd213pd %ymm0, %ymm7, %ymm8 #41.35
vfmadd213pd %ymm0, %ymm7, %ymm2 #42.35
vfmadd213pd %ymm0, %ymm7, %ymm3 #43.35
vfmadd213pd %ymm0, %ymm7, %ymm4 #44.35
vfmadd213pd %ymm0, %ymm7, %ymm5 #45.35
vfmadd213pd %ymm0, %ymm7, %ymm6 #46.35
vfmadd213pd %ymm0, %ymm7, %ymm1 #47.35
cmpl $1000000000, %eax #35.5
jb ..B1.24 # Prob 99% #35.5Listing 11: Lines from Fused Multiply Add example assembly code on Broadwell.
The generated assembly for Skylake looks like in the listing below. It also uses the vfmadd213pd instruction, but ZMM are the 512-bit AVX-512 registers. Therefore, every instruction processes eight double precision numbers.
..B1.24: # Preds ..B1.24 ..B1.23
# Execution count [1.00e+06]
incl %eax #33.5
vfmadd213pd %zmm0, %zmm1, %zmm9 #36.35
vfmadd213pd %zmm0, %zmm1, %zmm8 #37.35
vfmadd213pd %zmm0, %zmm1, %zmm7 #38.35
vfmadd213pd %zmm0, %zmm1, %zmm6 #39.35
vfmadd213pd %zmm0, %zmm1, %zmm5 #40.35
vfmadd213pd %zmm0, %zmm1, %zmm4 #41.35
vfmadd213pd %zmm0, %zmm1, %zmm3 #42.35
vfmadd213pd %zmm0, %zmm1, %zmm2 #43.35
cmpl $1000000000, %eax #33.5
jb ..B1.24 # Prob 99% #33.5Listing 12: Lines from Fused Multiply Add example assembly code on Skylake.
We measured the performance of these codes on two systems:
- Intel Xeon processor 2699 v4 (Broadwell) with 2 sockets, each socket with 22 cores at 2.2 GHz and
- Intel Xeon Platinum 8160 processor (Skylake) with 2 sockets, each socket with 24 cores at 2.1 GHz.
On both systems we turned off the Intel® Turbo Boost technology by disabling the intel_pstate driver via a kernel argument (to fall back to the acpi-cpufreq driver) and setting the CPUfreq governor “userspace” combined with a fixed clock frequency of 2.2~GHz on Broadwell and 2.1~GHz on Skylake.
Our measurements were taken for a set of codes with the number of chained FMAs ranging from 1 (no chaining) to 35 (too many to fit even in the Skylake register file). We set the environment variable KMP_HW_SUBSET=1t, which results in 44 OpenMP threads on Broadwell and 48 threads on Skylake, and KMP_AFFINITY=compact,1, which places one thread on each physical core.
The results are shown in the figure below.
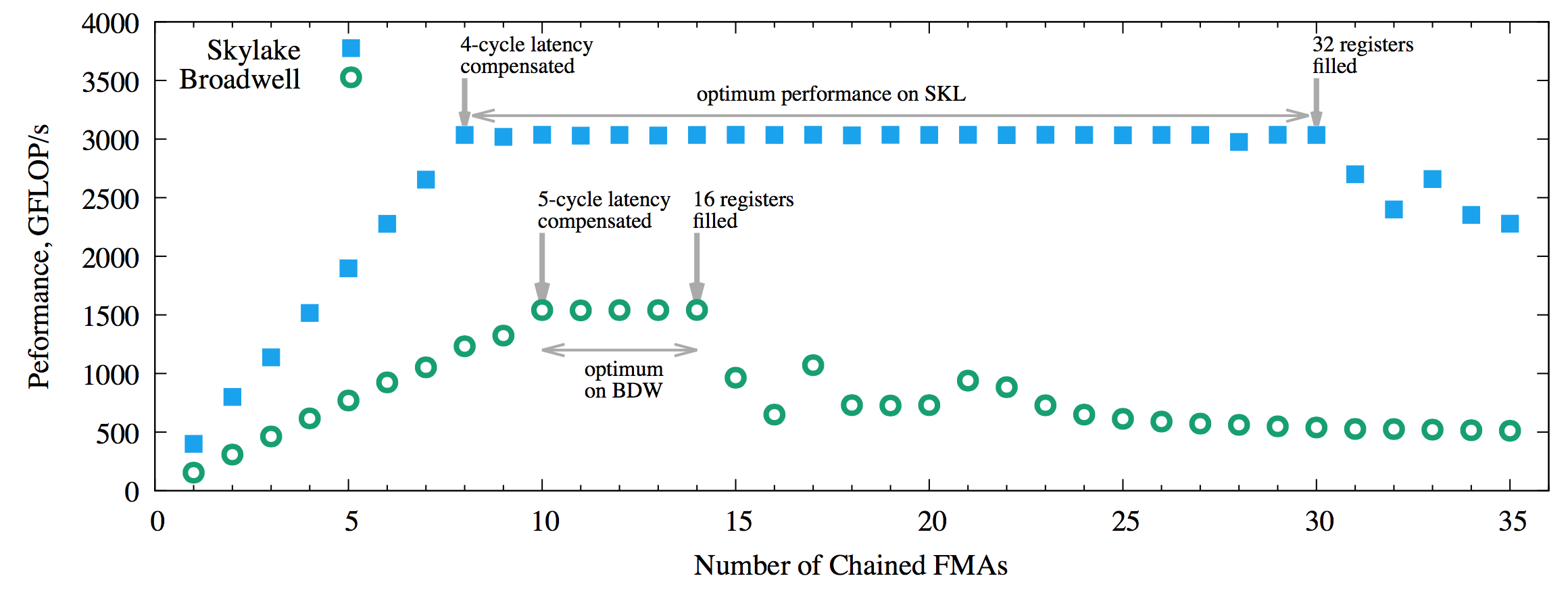
Figure 2: Performance of the FMA benchmark on Broadwell and Skylake architecture processors with 1 thread/core.
We observe the optimum performance on Broadwell for the number of chained FMAs between 10 and 14. This range is consistent with our theoretical predictions. The best performance that we measured is 1540 GFLOP/s.
Skylake achieves the optimum performance for the number of chained FMAs between 8 and 30. This range is also in agreement with our theoretical expectations. The best performance on Skylake is 3030 GFLOP/s.
The range of well-performing values for n_chained_fmas is much wider on Skylake than on Broadwell due to a lower latency of FMA and a larger register file on SKL. This fact is important for performance tuning strategy: instead of trying to contain the traffic of reusable data in caches, you can have better results by reusing data in the register file.
In cases when you do not have enough independent instructions to populate the pipeline, you can use the Intel® Hyper-Threading technology. This technology allows each core in the CPU to present itself as two (for Intel Xeon processors) or four (for Intel Xeon Phi processors) logical processors, each of which is designed to execute a single thread. The instruction decode unit in the core can pipeline instructions from all logical processors in a core. Therefore, with two threads per core on Intel Xeon Processors or two to four on Intel Xeon Phi processors, you can achieve the plateau of peak performance with fewer chained instructions. The same approach can be used to mask the latency of memory accesses when fully containing memory traffic to caches or registers is not possible or practical.
The figure below shows the performance benchmark of FMA, this time measured with two threads per core by setting KMP_HW_SUBSET=2t, which results in 88 threads on Skylake and 96 on Broadwell.
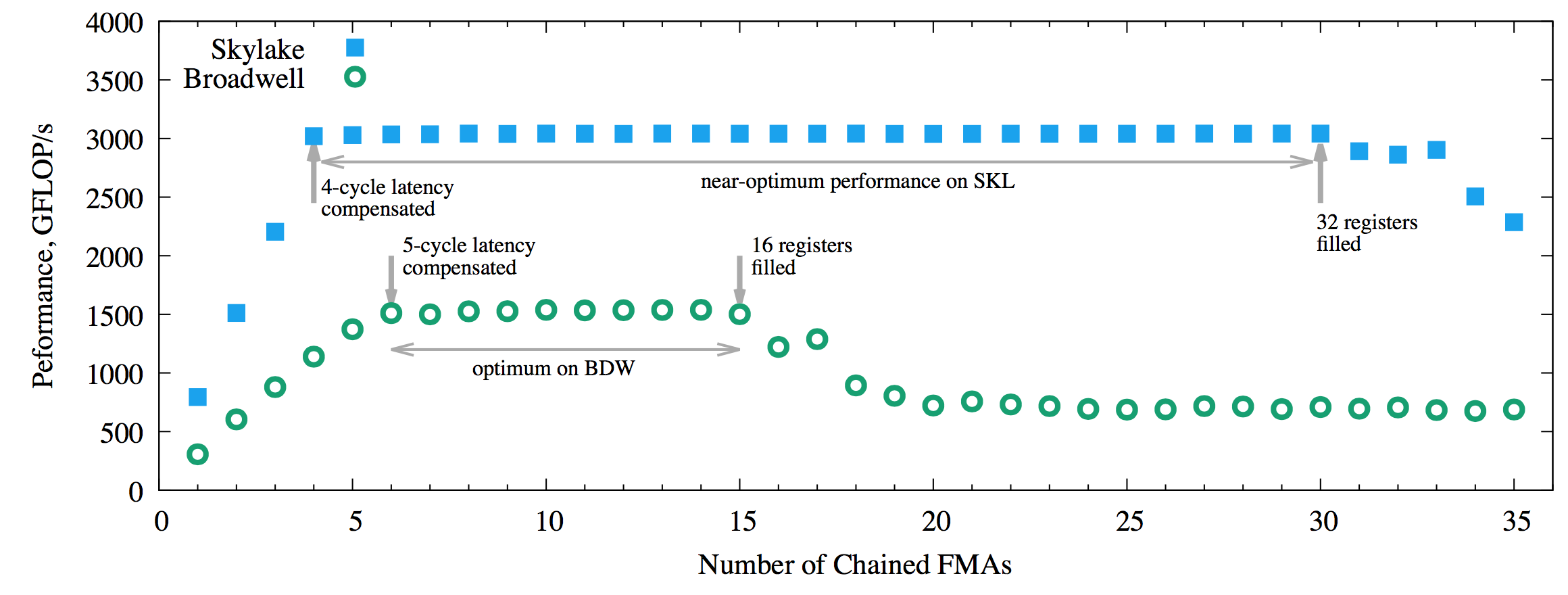
Figure 3: Performance of the FMA benchmark on Broadwell and Skylake architecture processors with 2 threads/core.
In this case, we can see the plateau achieved with just 4 and 6 chained FMAs on Skylake and Broadwell, respectively. However, the level of the plateau on Skylake stays around 10% lower than the optimum until the number of chained FMAs reaches 16. We attribute this effect to the overhead of the hyper-threading technology.
2.2. Clock Frequency and Peak Performance
Now we should estimate the theoretical peak performance to make sure that the measured numbers make sense. The peak performance for a single instruction (we will denote it as P) can be estimated as
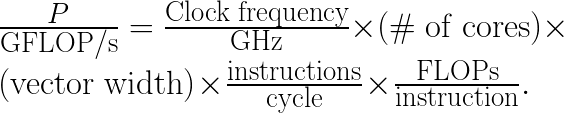
In the case of FMA, FLOPs/instruction=2 by definition, and the throughput instructions/cycle=2 in both our systems. So for our Broadwell CPU (Intel Xeon processor E5-2699 v4),
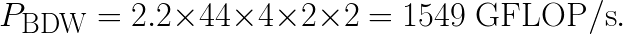
For the Skylake CPU (Intel Xeon Platinum processor 8160), the base frequency listed in the CPU specifications is 2.1 GHz. However, this frequency is applicable only to non-AVX workloads. For workloads heavy in AVX-512, like our benchmark, the CPU reduces the clock frequency. According to Intel Xeon processor Scalable family specification, page 15, when all cores are heavily utilized with AVX-512, the processor clocks down to 2.0 GHz, making
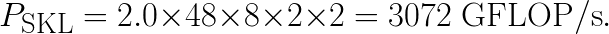
These peak performance estimates are only marginally higher than our measurements for Broadwell and Skylake, 1540 and 3030 GFLOP/s, respectively. Quantitatively, our efficiency in both cases is 99%.
At the same time, both processors are capable of frequency scaling thanks to the Intel Turbo Boost technology. The maximum turbo frequency for Intel Xeon processor E5-2699 v4 is 3.6 GHz and for Intel Xeon Platinum processor 8160 it is equal to 3.7 GHz. If the Intel Turbo Boost technology is enabled in the BIOS, and the CPUfreq governor in the Linux kernel allows frequency scaling, the runtime frequency may be greater than the base clock frequency, up to the maximum Turbo frequency. We ran the benchmark without modification on the Broadwell processor with enabled frequency scaling, and in the optimum case, the cores settled into a clock frequency of 2.6 GHz and delivered a maximum performance of 1940 GFLOP/s, which is 26% greater than the measurement without frequency scaling. On Skylake, cores settled into a clock frequency of 2.0 GHz, producing the nearly same performance as without frequency scaling, 3040~GFLOP/s.
We will not discuss clock frequencies further in this publication, as this subject is only indirectly related to the changes in the instruction set. We may cover this topic in a different paper.
Finally, regarding the throughput of FMA, it is important to mention that our Skylake processor delivered a throughput of two FMA instructions per cycle because it had two FMA units ported to port 0 and 5. Some other processors based on the Skylake architecture may have a single FMA unit located on port 0. The lack of a second FMA unit reduces the throughput expectation to one instruction per cycle. More details can be found in Section 13.20 of the Intel® 64 and IA-32 Architectures Optimization Reference Manual.
2.3. AVX-512CD: Conflict Detection
The conflict detection instruction introduced in AVX-512CD operates on a vector of memory addresses or integers. It returns the set of vector lanes that contain elements equal to any other elements in this vector. This instruction, along with a few other support instructions of AVX-512CD, allows the vectorization of codes with indirect memory accesses leading to write conflicts. Binning (histogram data computation) is an example of such workloads. Binning was not fully vectorizable in earlier instruction sets (see, e.g., this paper).
The figure below illustrates the workflow of the microkernel A[B[i]]+=1, where i ranges from 0 to n-1.
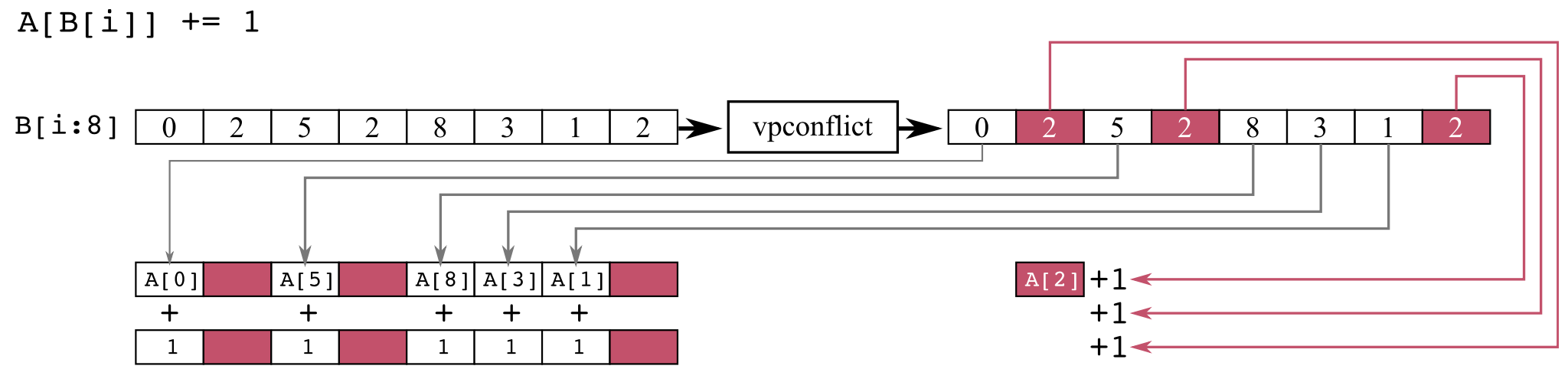
Figure 4: Histogram data computation with conflict detection
For older instruction sets (e.g., AVX/AVX2), this kernel must be executed sequentially, i.e., one value of i per instruction. Indeed, if the offset B[i] has the same value for different values of i, then the corresponding values of A must be incremented several times. In contrast, for AVX-512CD, Intel compilers implement a procedure that consists of three steps. First, the code loads a block of values from B in a vector register, and a conflict detection instruction identifies vector lanes in which the values (offsets) are identical, i.e., in conflict. Second, the code increments the values of A corresponding to non-conflicting values of i in parallel with a vector addition instruction. Third, the code sequentially increments the values of A corresponding to conflicting values of i. In the last step, sequential execution is necessary to produce correct results. However, in the second step, parallelism is acceptable, and vectorization of this step may yield performance gains compared to sequential execution, especially if the frequency of conflicts is low.
Let’s study this new functionality with an example. The for-loop in the listing below is an example of a vector dependence due to the possible writing conflict in adjacent iterations, which makes it impossible to vectorize on the Broadwell microarchitecture.
const int ARR_SIZE=8000;
int main() {
float A[ARR_SIZE],C[ARR_SIZE];
int B[ARR_SIZE];
int i;
for(i = 0; i < ARR_SIZE; i++)
A[B[i]] += 1.0f/C[i];
}Listing 13: Loop with conflicts and vector dependencies.
To compile the example for Broadwell, use command lines in the listing below with -xCORE-AVX2.
icc CD.c -xCORE-AVX2 -O3 -qopt-report=5 -fp-model fast=2 -SListing 14: Compilation lines for conflict detection example (Broadwell).
This command produces an optimization report and assembly file. In the case of Broadwell, according to the optimization report in the listing below, the loop was not vectorized due to a vector dependence (i.e., operations a block of values of i cannot be performed in parallel using vector instructions).
LOOP BEGIN at CD.c(9,3)
remark #15344: loop was not vectorized: vector dependence prevents vectorization
remark #15346: vector dependence: assumed FLOW dependence between A[B[i]] (10:5) and A[B[i]] (10:5)
remark #15346: vector dependence: assumed ANTI dependence between A[B[i]] (10:5) and A[B[i]] (10:5)
remark #25438: unrolled without remainder by 4
remark #25456: Number of Array Refs Scalar Replaced In Loop: 4
LOOP ENDListing 15: Optimization report for conflict detection example on Broadwell.
The associated assembly code in the listing below shows that the loop was not vectorized, and it was implemented on the lower 128 bits (XMM) of the vector registers.
..B1.2: # Preds ..B1.2 ..B1.6
# Execution count [2.00e+03]
vdivss 64000(%rsp,%rax), %xmm0, %xmm1 #10.21
vdivss 64004(%rsp,%rax), %xmm0, %xmm3 #10.21
vdivss 64008(%rsp,%rax), %xmm0, %xmm5 #10.21
vdivss 64012(%rsp,%rax), %xmm0, %xmm7 #10.21
movslq 32000(%rsp,%rax), %rcx #10.7
incl %edx #9.3
movslq 32004(%rsp,%rax), %rdi #10.7
movslq 32008(%rsp,%rax), %r9 #10.7
movslq 32012(%rsp,%rax), %r10 #10.7
lea (,%rcx,4), %rsi #10.5
addq $16, %rax #9.3
lea (,%rdi,4), %r8 #10.5
vaddss (%rsp,%rcx,4), %xmm1, %xmm2 #10.5
vmovss %xmm2, (%rsp,%rsi) #10.5
vaddss (%rsp,%rdi,4), %xmm3, %xmm4 #10.5
vmovss %xmm4, (%rsp,%r8) #10.5
vaddss (%rsp,%r9,4), %xmm5, %xmm6 #10.5
vmovss %xmm6, (%rsp,%r9,4) #10.5
vaddss (%rsp,%r10,4), %xmm7, %xmm8 #10.5
vmovss %xmm8, (%rsp,%r10,4) #10.5
cmpl $2000, %edx #9.3
jb ..B1.2 # Prob 99% #9.3
# LOE rax rbx r12 r13 r14 r15 edx xmm0Listing 16: Lines from assembly code for compiling conflict detection example on Broadwell.
To compile the code for Skylake, use the command in the listing below with -xCORE-AVX512.
icc CD.c -xCORE-AVX512 -O3 -qopt-report=5 -fp-model fast=2 -SListing 17: Compilation lines for conflict detection example (Skylake).
In the case of Skylake, the optimization report in the listing below shows that the loop was vectorized and that the vector dependencies were resolved by recognizing a histogram calculation pattern.
LOOP BEGIN at CD.c(9,3)
remark #15388: vectorization support: reference B[i] has aligned access [ CD.c(10,7) ]
remark #15388: vectorization support: reference B[i] has aligned access [ CD.c(10,7) ]
remark #15388: vectorization support: reference C[i] has aligned access [ CD.c(10,21) ]
remark #15416: vectorization support: irregularly indexed store was generated for the variable <A[B[i]]>, part of index is read from memory [ CD.c(10,5) ]
remark #15415: vectorization support: irregularly indexed load was generated for the variable <A[B[i]]>, part of index is read from memory [ CD.c(10,5) ]
remark #15305: vectorization support: vector length 16
remark #15300: LOOP WAS VECTORIZED
remark #15448: unmasked aligned unit stride loads: 2
remark #15462: unmasked indexed (or gather) loads: 1
remark #15463: unmasked indexed (or scatter) stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 36
remark #15477: vector cost: 16.810
remark #15478: estimated potential speedup: 2.140
remark #15486: divides: 1
remark #15488: --- end vector cost summary ---
remark #15499: histogram: 2
remark #25015: Estimate of max trip count of loop=500
LOOP BEGIN at
remark #25460: No loop optimizations reported
LOOP END
LOOP ENDListing 18: Optimization report for conflict detection example on Skylake.
According to the optimization report, the potential speedup of the loop vectorization on Skylake is 2.14 compared to scalar code. Note that speedups in the optimization report are estimated relative to scalar code on the same architecture and cannot be used to compare the estimated performance between architectures.
In the listing below we show the assembly for the Skylake code.
..B1.2: # Preds ..B1.6 ..B1.10
# Execution count [0.00e+00]
vmovups 32064(%rsp,%rcx,4), %zmm2 #10.21
vrcp14ps %zmm2, %zmm1 #10.21
vmulps %zmm2, %zmm1, %zmm2 #10.21
vaddps %zmm1, %zmm1, %zmm4 #10.21
vfnmadd213ps %zmm4, %zmm1, %zmm2 #10.21
vmovups 64064(%rsp,%rcx,4), %zmm4 #10.7
kmovw %k1, %k2 #10.5
vpconflictd %zmm4, %zmm1 #10.5
vptestmd .L_2il0floatpacket.1(%rip), %zmm1, %k0 #10.5
kmovw %k0, %eax #10.5
vpxord %zmm0, %zmm0, %zmm0 #10.5
vgatherdps (%rdx,%zmm4,4), %zmm0{%k2} #10.5
vaddps %zmm2, %zmm0, %zmm3 #10.5
testl %eax, %eax #10.5
je ..B1.6 # Prob 30% #10.5
# LOE rdx rcx rbx r12 r13 r14 r15 zmm1 zmm2 zmm3 zmm4 k1
..B1.3: # Preds ..B1.2
# Execution count [0.00e+00]
vpbroadcastmw2d %k1, %zmm6 #10.5
vplzcntd %zmm1, %zmm5 #10.5
vmovups .L_2il0floatpacket.2(%rip), %zmm0 #10.5
vptestmd %zmm1, %zmm6, %k0 #10.5
vpsubd %zmm5, %zmm0, %zmm0 #10.5
kmovw %k0, %eax #10.5
# LOE rdx rcx rbx r12 r13 r14 r15 eax zmm0 zmm1 zmm2 zmm3 zmm4 k1
..B1.4: # Preds ..B1.4 ..B1.3
# Execution count [0.00e+00]
kmovw %eax, %k2 #10.5
vpbroadcastmw2d %k2, %zmm5 #10.5
vpermps %zmm3, %zmm0, %zmm3{%k2} #10.5
vptestmd %zmm1, %zmm5, %k0{%k2} #10.5
vaddps %zmm2, %zmm3, %zmm3{%k2} #10.5
kmovw %k0, %eax #10.5
testl %eax, %eax #10.5
jne ..B1.4 # Prob 70% #10.5
# LOE rdx rcx rbx r12 r13 r14 r15 eax zmm0 zmm1 zmm2 zmm3 zmm4 k1
..B1.6: # Preds ..B1.4 ..B1.2
# Execution count [8.00e+03]
addq $16, %rcx #9.3
kmovw %k1, %k2 #10.5
vscatterdps %zmm3, (%rdx,%zmm4,4){%k2} #10.5
cmpq $8000, %rcx #9.3
jb ..B1.2 # Prob 99% #9.3
# LOE rdx rcx rbx r12 r13 r14 r15 k1Listing 19: Lines from assembly code for compiling conflict detection example on Skylake.
In block B1.2, the vpconflictd instruction compares each element of the vector register with all previous elements in that register and outputs the results of all comparisons. If there are no conflicts, the code jumps to block B1.6, where the resulting vector is scattered into array A. Otherwise (i.e., in case of conflicts), the code makes preparation work in B1.3 and sets up a loop in B1.4 over the conflicted vector lanes. After that, in B1.6, the resulting vector with the correctly incremented vector lanes is written back to memory.
2.4. AVX-512F: Masking
Masking in AVX-512 is supported by a set of eight 64-bit opmask registers. Masking registers conditionally control computational operations and updates of the destination vector with per-element granularity. The purpose of masked operations is vectorization of loops with if-statements.
The AVX-512 masking support is an improvement over AVX2. Masking in AVX2 uses one of the 256-bit YMM vector registers to hold the mask. AVX2 load, store, gather and blend operations accept the mask register explicitly, and masked memory access may be sufficient for simple cases. Other AVX2 instructions do not explicitly support masking, but in more complex cases, the compiler can emulate masking in other instructions by performing unmasked arithmetic followed by bitwise “and” with the mask register. These operations must be followed by a blend instruction. In contrast, AVX-512 masking uses dedicated bitmask registers, which do not occupy ZMM space. Most AVX-512 instructions accept a mask explicitly, so following up with bitwise “and” is not neccessary. Additionally, AVX-512 masking is enabled for 128, 256 and 512-bit vector length, and supports all data types: byte, word, double and quad-word.
The figure below demonstrates the difference between the implementation of masking in AVX2 and AVX-512 for the kernel “if (B[i] < 0.0) B[i]*=0.1“.
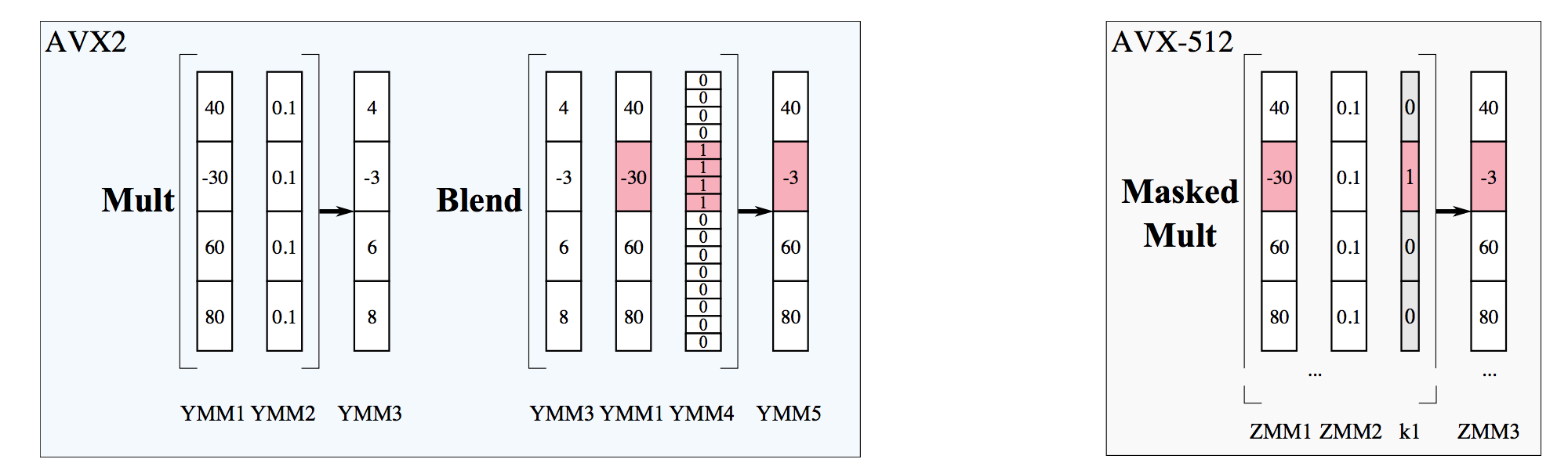
Figure 5: Illustration of the difference between masking functionality in AVX2 and AVX-512.
In AVX2, the mask is stored in a YMM data register, while in AVX-512 it is stored in a bitmask register k1. AVX2 requires two operations: unmasked multiplication and blending, while AVX-512 uses only one masked multiplication. AVX2 uses five data registers, while AVX-512 uses three data registers and one bitmask register.
The listing below contains an example of a loop that the Intel compiler can vectorize with the help of masking.
void ConditionalLoop(double * restrict A, double * restrict B, double * restrict C) {
int i;
for( i = 0; i < 10000; i++ ) {
if(B[i] > 0.0)
A[i] *= B[i];
else
A[i] += B[i];
}
}Listing 20: Masking example.
The listing below shows the assembly for this code compiled for the Broadwell target. The compiler unrolls the loop and for each vector iteration implements arithmetics (vmulpd, vaddpd), comparison (vcmpgtpd), and masking (vxorpd, vandpd and vblendvpd).
..B1.11: # Preds ..B1.11 ..B1.10
vmovupd (%rsi,%rdx,8), %ymm5 #4.8
vmovupd 32(%rsi,%rdx,8), %ymm13 #4.8
vmovupd 32(%rdi,%rdx,8), %ymm12 #7.7
vmovupd (%rdi,%rdx,8), %ymm4 #7.7
vcmpgtpd %ymm1, %ymm5, %ymm8 #4.15
vmulpd %ymm13, %ymm12, %ymm15 #5.7
vmulpd %ymm5, %ymm4, %ymm7 #5.7
vxorpd %ymm8, %ymm0, %ymm2 #4.15
vandpd %ymm2, %ymm5, %ymm3 #7.15
vcmpgtpd %ymm1, %ymm13, %ymm2 #4.15
vaddpd %ymm3, %ymm4, %ymm6 #7.7
vxorpd %ymm2, %ymm0, %ymm10 #4.15
vandpd %ymm10, %ymm13, %ymm11 #7.15
vaddpd %ymm11, %ymm12, %ymm14 #7.7
vblendvpd %ymm8, %ymm7, %ymm6, %ymm9 #7.7
vblendvpd %ymm2, %ymm15, %ymm14, %ymm3 #7.7
vmovupd 96(%rsi,%rdx,8), %ymm15 #4.8
vmovupd 64(%rsi,%rdx,8), %ymm7 #4.8
vmovupd 64(%rdi,%rdx,8), %ymm6 #7.7
vmovupd 96(%rdi,%rdx,8), %ymm14 #7.7
vmovupd %ymm9, (%rdi,%rdx,8) #5.7
vmovupd %ymm3, 32(%rdi,%rdx,8) #5.7
vmulpd %ymm7, %ymm6, %ymm9 #5.7
vcmpgtpd %ymm1, %ymm15, %ymm2 #4.15
vcmpgtpd %ymm1, %ymm7, %ymm10 #4.15
vxorpd %ymm2, %ymm0, %ymm12 #4.15
vandpd %ymm12, %ymm15, %ymm13 #7.15
vxorpd %ymm10, %ymm0, %ymm4 #4.15
vaddpd %ymm13, %ymm14, %ymm12 #7.7
vmulpd %ymm15, %ymm14, %ymm13 #5.7
vandpd %ymm4, %ymm7, %ymm5 #7.15
vaddpd %ymm5, %ymm6, %ymm8 #7.7
vblendvpd %ymm2, %ymm13, %ymm12, %ymm3 #7.7
vblendvpd %ymm10, %ymm9, %ymm8, %ymm11 #7.7
vmovupd %ymm3, 96(%rdi,%rdx,8) #5.7
vmovupd %ymm11, 64(%rdi,%rdx,8) #5.7
addq $16, %rdx #3.3
cmpq %rax, %rdx #3.3
jb ..B1.11 # Prob 99% #3.3Listing 21: Lines of assembly code for compiling masking example on Broadwell.
The listing below shows the optimization report for the Broadwell target.
LOOP BEGIN at MA.c(3,3)
remark #15300: LOOP WAS VECTORIZED
remark #15448: unmasked aligned unit stride loads: 1
remark #15449: unmasked aligned unit stride stores: 1
remark #15450: unmasked unaligned unit stride loads: 1
remark #15476: scalar cost: 20
remark #15477: vector cost: 5.500
remark #15478: estimated potential speedup: 3.620
remark #25015: Estimate of max trip count of loop=625
LOOP ENDListing 22: Abridged optimization report for masking example on Broadwell.
For Skylake, the compiler produces a simpler assembly as shown in the listing below.
..B1.8: # Preds ..B1.8 ..B1.7
vmovups (%rsi,%rcx,8), %zmm3 #4.8
vmovups 64(%rsi,%rcx,8), %zmm7 #4.8
vmovups 128(%rsi,%rcx,8), %zmm11 #4.8
vmovups 192(%rsi,%rcx,8), %zmm15 #4.8
vmovups (%rdi,%rcx,8), %zmm2 #7.7
vmovups 64(%rdi,%rcx,8), %zmm6 #7.7
vmovups 128(%rdi,%rcx,8), %zmm10 #7.7
vmovups 192(%rdi,%rcx,8), %zmm14 #7.7
vcmppd $6, %zmm0, %zmm3, %k2 #4.15
vcmppd $6, %zmm0, %zmm7, %k4 #4.15
vcmppd $6, %zmm0, %zmm11, %k6 #4.15
knotw %k2, %k1 #7.15
knotw %k4, %k3 #7.15
knotw %k6, %k5 #7.15
vmovapd %zmm3, %zmm1{%k1}{z} #7.15
vcmppd $6, %zmm0, %zmm15, %k1 #4.15
vaddpd %zmm1, %zmm2, %zmm4 #7.7
knotw %k1, %k7 #7.15
vmulpd %zmm3, %zmm2, %zmm4{%k2} #5.7
vmovapd %zmm7, %zmm5{%k3}{z} #7.15
vmovapd %zmm11, %zmm9{%k5}{z} #7.15
vmovapd %zmm15, %zmm13{%k7}{z} #7.15
vaddpd %zmm5, %zmm6, %zmm8 #7.7
vaddpd %zmm9, %zmm10, %zmm12 #7.7
vaddpd %zmm13, %zmm14, %zmm16 #7.7
vmulpd %zmm7, %zmm6, %zmm8{%k4} #5.7
vmulpd %zmm11, %zmm10, %zmm12{%k6} #5.7
vmulpd %zmm15, %zmm14, %zmm16{%k1} #5.7
vmovupd %zmm4, (%rdi,%rcx,8) #5.7
vmovupd %zmm8, 64(%rdi,%rcx,8) #5.7
vmovupd %zmm12, 128(%rdi,%rcx,8) #5.7
vmovupd %zmm16, 192(%rdi,%rcx,8) #5.7
addq $32, %rcx #3.3
cmpq %rdx, %rcx #3.3
jb ..B1.8 # Prob 99% #3.3Listing 23: Lines of assembly code for compiling masking example on Skylake.
This AVX-512 code writes the result of the comparison in the if-statement condition (vcmppd) into masks k2, k4, k6 and k1, and the multiplication instruction vmulpd uses this bitmask. The intermediate store instructions vmovapd use the inverse of the masks stored in k1, k3, k5 and k7 (similar to vpblendvpd in AVX2), and eventually the data is written to memory by vmovupd without masking.
The optimization report for the Skylake target is shown in the listing below.
LOOP BEGIN at MA.c(3,3)
remark #15300: LOOP WAS VECTORIZED
remark #15448: unmasked aligned unit stride loads: 1
remark #15449: unmasked aligned unit stride stores: 1
remark #15450: unmasked unaligned unit stride loads: 1
remark #15476: scalar cost: 20
remark #15477: vector cost: 2.870
remark #15478: estimated potential speedup: 6.930
remark #25015: Estimate of max trip count of loop=312
LOOP ENDListing 24: Abridged optimization report for masking example on Skylake.
In addition to loop unrolling by a factor of 4, you can notice that instructions in the unrolled iterations are permuted. Eight loads (vmovups) are followed by three comparisons (vcmppd) and bitmask manipulation (knotw), and the fourth comparison comes later. Similar permutations are seen in masked additions (vaddpd) and multiplications (vmulpd). The compiler does not report the motivation for permutation. However, we speculate that it optimally packs the pipeline of the Skylake architecture core.
Interestingly, when we compiled the code for Knights Landing with -xMIC-AVX512, the compiler chose an unroll factor of 2 instead of 4 and also changed the instruction permutation strategy. The resulting assembly for KNL is shown in the listing below.
..B1.8: # Preds ..B1.8 ..B1.7
vcmppd $9, (%rsi,%rcx,8), %zmm0, %k2 #4.15 c1
vcmppd $9, 64(%rsi,%rcx,8), %zmm0, %k4 #4.15 c1
knotw %k2, %k1 #7.15 c3
knotw %k4, %k3 #7.15 c3
vmovups (%rdi,%rcx,8), %zmm2 #7.7 c3
vmovups 64(%rdi,%rcx,8), %zmm5 #7.7 c3
vmovupd (%rsi,%rcx,8), %zmm1{%k1}{z} #7.15 c9 stall 2
vmovupd 64(%rsi,%rcx,8), %zmm4{%k3}{z} #7.15 c9
vaddpd (%rdi,%rcx,8), %zmm1, %zmm3 #7.7 c15 stall 2
vaddpd 64(%rdi,%rcx,8), %zmm4, %zmm6 #7.7 c15
vmulpd (%rsi,%rcx,8), %zmm2, %zmm3{%k2} #5.7 c21 stall 2
vmovupd %zmm3, (%rdi,%rcx,8) #5.7 c27 stall 2
vmulpd 64(%rsi,%rcx,8), %zmm5, %zmm6{%k4} #5.7 c27
vmovupd %zmm6, 64(%rdi,%rcx,8) #5.7 c33 stall 2
addq $16, %rcx #3.3 c33
cmpq %rdx, %rcx #3.3 c35
jb ..B1.8 # Prob 99% #3.3 c37Listing 25: Lines of assembly code for compiling masking example for Knights Landing.
The differences between AVX-512 code for Skylake and Knights Landing further demonstrate that in the process of automatic vectorization, the compiler uses not only the instruction set of the target architecture but also the low-level technical details of the architecture organization, particularly pipelining.
2.5. AVX-512F: Compress/Expand
AVX-512F in Skylake enables the vectorization of the data compress and expand operations. The vcompress instruction reads elements from the input register using a read mask and writes them contiguously into the output register. The vexpand instruction does the opposite: reads adjacent elements from the input register and stores them in the destination register according to the write mask. These instructions are useful for compressing a subset of data into a compact new container or doing the opposite.
The listing below shows an example for compressing data with non-zero values.
void Compress(float* restrict A, float* restrict B) {
int i;
#pragma nounroll // Not needed in real-world calculation; used here to simplify assembly
for( i = 0; i < 8000; i++ ) {
if(A[i] != 0)
B[j++] = A[i];
}
}Listing 26: Data compress example.
The compress operation in this code is implemented differently for AVX2 and AVX-512. In AVX2, the compiler does not vectorize the data compression loop. The listing below shows the AVX2 assembly.
..B1.4: # Preds ..B1.6 ..B1.3
# Execution count [8.00e+03]
vmovss (%rdi,%rax,4), %xmm1 #5.8
vucomiss %xmm0, %xmm1 #5.16
jp ..B1.5 # Prob 0% #5.16
je ..B1.6 # Prob 16% #5.16
# LOE rax rdx rbx rbp rsi rdi r12 r13 r14 r15 xmm0 xmm1
..B1.5: # Preds ..B1.4
# Execution count [6.72e+03]
vmovss %xmm1, (%rsi,%rdx,4) #6.7
incq %rdx #6.9
# LOE rax rdx rbx rbp rsi rdi r12 r13 r14 r15 xmm0
..B1.6: # Preds ..B1.5 ..B1.4
# Execution count [8.00e+03]
incq %rax #4.25
cmpq $8000, %rax #4.19
jl ..B1.4 # Prob 99% #4.19Listing 27: Lines from assembly code for compiling data compress example on Broadwell.
The loop processes one element of A at a time because vmovss is a scalar load operation. The vucomiss operation performs a comparison of A[i] with 0, and the subsequent code either stores it in B (block B1.5) or skips it (block B1.6).
The optimization report in the listing below shows that vector dependence prevents vectorization, and the loop uses scalar instructions.
LOOP BEGIN at compress.c(4,3)
remark #15344: loop was not vectorized: vector dependence prevents vectorization
remark #15346: vector dependence: assumed FLOW dependence between j (6:9) and j (6:7)
remark #15346: vector dependence: assumed ANTI dependence between j (6:7) and j (6:9)
LOOP ENDListing 28: Lines from optimization report for data compress example on Broadwell.
When we compiled the code for Skylake (AVX-512), the loop was vectorized. The listing below shows the assembly. The compress operation is performed directly using the vcompressps instruction. It copies and compresses up to 16 single precision floating-point values into the destination operand using the source operand ZMM1 and the opmask register k1. The opmask register selects the elements from the source that get copied and compressed.
..B1.16: # Preds ..B1.18 ..B1.15
# Execution count [0.00e+00]
vmovups (%rdi,%rax,4), %zmm1 #5.8
vpxord %zmm0, %zmm0, %zmm0 #5.16
vcmpps $4, %zmm0, %zmm1, %k1 #5.16
kmovw %k1, %r9d #5.16
testl %r9d, %r9d #5.16
je ..B1.18 # Prob 20% #5.16
# LOE rax rdx rbx rbp rdi r8 r12 r13 r14 r15 ecx esi r9d zmm1 k1
..B1.17: # Preds ..B1.16
# Execution count [8.00e+03]
movslq %ecx, %rcx #6.7
popcnt %r9d, %r9d #6.7
vcompressps %zmm1, (%r8,%rcx,4){%k1} #6.7
addl %r9d, %ecx #6.7
# LOE rax rdx rbx rbp rdi r8 r12 r13 r14 r15 ecx esi
..B1.18: # Preds ..B1.17 ..B1.16
# Execution count [8.00e+03]
addq $16, %rax #4.3
cmpq %rdx, %rax #4.3
jb ..B1.16 # Prob 99% #4.3Listing 29: Lines from assembly code for compiling data compress example on Skylake.
The optimization report in the listing below shows that the loop was vectorized and that the compiler detects one compress operation. The estimated potential speedup is 22.0 compared to scalar code.
LOOP BEGIN at compress.c(4,3)
remark #15300: LOOP WAS VECTORIZED
remark #15442: entire loop may be executed in remainder
remark #15448: unmasked aligned unit stride loads: 1
remark #15457: masked unaligned unit stride stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 18
remark #15477: vector cost: 0.810
remark #15478: estimated potential speedup: 22.000
remark #15488: --- end vector cost summary ---
remark #15497: vector compress: 1
remark #25015: Estimate of max trip count of loop=500
LOOP ENDListing 30: Lines from the optimization report for data compress example on Skylake.
2.6. AVX-512F: New Shuffle Instructions
AVX-512 on Skylake introduces a new set of shuffle instructions that allow you to rearrange elements in one or two source registers and write them to the destination register. These instructions are supported for different element sizes: byte, word, double and quadword.
The listing below shows a function that performs a transposition of an 8×8 matrix of double precision floating-point numbers.
void Transpose8x8(double * restrict A, double * restrict B) {
int i, j;
for (i = 0; i < 8; i++)
for (j = 0; j < 8; j++)
A[i*8 + j] = B[j*8 + i];
}Listing 31: Matrix transposition example.
We compiled the code with AVX2 using the compilation line in the listing below.
icc PR.c -S -vec-threshold0 -xCORE-AVX2 -qopt-report=5 Listing 32: Compilation commands for matrix transposition example (Broadwell).
The optimization report in the listing below shows a potential speedup of 1.48 due to vectorization.
LOOP BEGIN at PR.c(4,5)
remark #15389: vectorization support: reference A[i*8+j] has unaligned access [ PR.c(5,7) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15328: vectorization support: non-unit strided load was emulated for the variable <B[j*8+i]>, stride is 8 [ PR.c(5,20) ]
remark #15305: vectorization support: vector length 4
remark #15427: loop was completely unrolled
remark #15399: vectorization support: unroll factor set to 2
remark #15309: vectorization support: normalized vectorization overhead 0.125
remark #15300: LOOP WAS VECTORIZED
remark #15451: unmasked unaligned unit stride stores: 1
remark #15452: unmasked strided loads: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 5
remark #15477: vector cost: 3.000
remark #15478: estimated potential speedup: 1.480
remark #15488: --- end vector cost summary ---
LOOP ENDListing 33: Optimization report for matrix transposition example on Broadwell.
Even though Broadwell can run this code with vector instructions, it is important to see how exactly the Intel compiler achieves this in AVX2. The listing below shows the assembly code for the matrix transpose example compiled with -xCORE-AVX2. This code shuffles elements using multiple vmovups and vinsertf128 instructions followed by vunpckhpd instruction. Instruction vunpckhpd unpacks and interleaves double precision floating-point elements from the source operand into the destination operand.
vmovups 16(%rsi), %xmm7 #5.20
vmovups 80(%rsi), %xmm9 #5.20
vmovups 64(%rsi), %xmm8 #5.20
vmovups (%rsi), %xmm6 #5.20
vmovups 256(%rsi), %xmm15 #5.20
vmovups 272(%rsi), %xmm1 #5.20
vmovups 320(%rsi), %xmm2 #5.20
vmovups 336(%rsi), %xmm0 #5.20
vinsertf128 $1, 144(%rsi), %ymm7, %ymm12 #5.20
vinsertf128 $1, 208(%rsi), %ymm9, %ymm13 #5.20
vunpcklpd %ymm13, %ymm12, %ymm5 #5.20
vmovupd %ymm5, 128(%rdi) #5.7
vmovups 96(%rsi), %xmm5 #5.20
vunpckhpd %ymm13, %ymm12, %ymm3 #5.20
vmovupd %ymm3, 192(%rdi) #5.7
vmovups 32(%rsi), %xmm3 #5.20
vinsertf128 $1, 128(%rsi), %ymm6, %ymm10 #5.20
vinsertf128 $1, 192(%rsi), %ymm8, %ymm11 #5.20
vunpcklpd %ymm11, %ymm10, %ymm14 #5.20
vunpckhpd %ymm11, %ymm10, %ymm4 #5.20
vmovupd %ymm14, (%rdi) #5.7
vmovupd %ymm4, 64(%rdi) #5.7
vmovups 48(%rsi), %xmm4 #5.20
vmovups 112(%rsi), %xmm14 #5.20
vinsertf128 $1, 384(%rsi), %ymm15, %ymm6 #5.20
vinsertf128 $1, 400(%rsi), %ymm1, %ymm8 #5.20
vinsertf128 $1, 448(%rsi), %ymm2, %ymm7 #5.20
vinsertf128 $1, 464(%rsi), %ymm0, %ymm9 #5.20
vunpcklpd %ymm7, %ymm6, %ymm10 #5.20
vunpckhpd %ymm7, %ymm6, %ymm11 #5.20
vunpcklpd %ymm9, %ymm8, %ymm12 #5.20
vunpckhpd %ymm9, %ymm8, %ymm13 #5.20
vmovups 304(%rsi), %xmm6 #5.20
vmovups 352(%rsi), %xmm7 #5.20
vmovups 368(%rsi), %xmm8 #5.20
vmovupd %ymm10, 32(%rdi) #5.7
vmovupd %ymm11, 96(%rdi) #5.7
vmovupd %ymm12, 160(%rdi) #5.7
vmovupd %ymm13, 224(%rdi) #5.7
vinsertf128 $1, 224(%rsi), %ymm5, %ymm2 #5.20
vmovups 288(%rsi), %xmm5 #5.20
vinsertf128 $1, 160(%rsi), %ymm3, %ymm1 #5.20
vinsertf128 $1, 176(%rsi), %ymm4, %ymm0 #5.20
vinsertf128 $1, 240(%rsi), %ymm14, %ymm3 #5.20
vunpcklpd %ymm2, %ymm1, %ymm4 #5.20
vinsertf128 $1, 416(%rsi), %ymm5, %ymm9 #5.20
vinsertf128 $1, 432(%rsi), %ymm6, %ymm11 #5.20
vinsertf128 $1, 480(%rsi), %ymm7, %ymm10 #5.20
vinsertf128 $1, 496(%rsi), %ymm8, %ymm12 #5.20
vunpckhpd %ymm2, %ymm1, %ymm1 #5.20
vunpcklpd %ymm3, %ymm0, %ymm2 #5.20
vunpckhpd %ymm3, %ymm0, %ymm0 #5.20
vmovupd %ymm4, 256(%rdi) #5.7
vmovupd %ymm1, 320(%rdi) #5.7
vmovupd %ymm2, 384(%rdi) #5.7
vmovupd %ymm0, 448(%rdi) #5.7
vunpcklpd %ymm10, %ymm9, %ymm13 #5.20
vunpckhpd %ymm10, %ymm9, %ymm15 #5.20
vunpcklpd %ymm12, %ymm11, %ymm3 #5.20
vunpckhpd %ymm12, %ymm11, %ymm4 #5.20
vmovupd %ymm13, 288(%rdi) #5.7
vmovupd %ymm15, 352(%rdi) #5.7
vmovupd %ymm3, 416(%rdi) #5.7
vmovupd %ymm4, 480(%rdi) #5.7Listing 34: Lines from assembly code for compiling the matrix transposition example for Broadwell.
In the case of Skylake, the compilation line in the listing below is used to compile the matrix transposition example code and produce an assembly file and an optimization report.
icc PR.c -S -vec-threshold0 -xCORE-AVX512 -qopt-report=5 Listing 35: Compilation commands for matrix transposition example (Skylake).
The optimization report in the listing below confirms that the loop was vectorized and shows an estimated potential speedup of 1.9 due to vectorization.
LOOP BEGIN at PR.c(4,5)
remark #15389: vectorization support: reference A[i*8+j] has unaligned access [ PR.c(5,7) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15415: vectorization support: non-unit strided load was generated for the variable <B[j*8+i]>, stride is 8 [ PR.c(5,20) ]
remark #15305: vectorization support: vector length 8
remark #15427: loop was completely unrolled
remark #15309: vectorization support: normalized vectorization overhead 0.167
remark #15300: LOOP WAS VECTORIZED
remark #15451: unmasked unaligned unit stride stores: 1
remark #15452: unmasked strided loads: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 5
remark #15477: vector cost: 2.250
remark #15478: estimated potential speedup: 1.900
remark #15488: --- end vector cost summary ---
LOOP ENDListing 36: Optimization report for matrix transposition example on Skylake.
On Skylake, vectorization takes advantage of the new shuffle instructions. The listing below shows the assembly for the matrix transposition example with the new AVX-512 instructions vpermt2q and vpermi2q. These instructions permute double precision floating-point numbers from ZMM registers and store the result back into the destination register. The following step is to blend and align the permuted data before storing it back. Instruction vpblendmq blends elements from ZMM registers using the opmask registers, and valignd merges vector registers.
vmovdqu32 (%rsi), %zmm20 #5.20
vmovdqu32 64(%rsi), %zmm7 #5.20
vmovdqu32 128(%rsi), %zmm16 #5.20
vmovdqu32 192(%rsi), %zmm9 #5.20
vmovdqu32 256(%rsi), %zmm19 #5.20
vmovdqu32 320(%rsi), %zmm11 #5.20
vmovdqu32 384(%rsi), %zmm18 #5.20
vmovdqu32 448(%rsi), %zmm13 #5.20
vmovdqu32 .L_2il0floatpacket.0(%rip), %zmm5 #5.20
vmovdqu32 .L_2il0floatpacket.1(%rip), %zmm2 #5.20
vmovdqu32 .L_2il0floatpacket.2(%rip), %zmm4 #5.20
vmovdqu32 .L_2il0floatpacket.3(%rip), %zmm3 #5.20
vmovdqu32 .L_2il0floatpacket.5(%rip), %zmm6 #5.20
vmovdqu32 .L_2il0floatpacket.6(%rip), %zmm8 #5.20
vmovdqu32 .L_2il0floatpacket.7(%rip), %zmm10 #5.20
vmovdqu32 .L_2il0floatpacket.8(%rip), %zmm12 #5.20
vmovdqu32 .L_2il0floatpacket.4(%rip), %zmm17 #5.20
vpermi2q %zmm7, %zmm20, %zmm5 #5.20
vpermi2q %zmm9, %zmm16, %zmm2 #5.20
vpermi2q %zmm11, %zmm19, %zmm4 #5.20
vpermi2q %zmm13, %zmm18, %zmm3 #5.20
vpermt2q %zmm7, %zmm6, %zmm20 #5.20
vpermt2q %zmm9, %zmm8, %zmm16 #5.20
vpermt2q %zmm11, %zmm10, %zmm19 #5.20
vpermt2q %zmm13, %zmm12, %zmm18 #5.20
kmovw %eax, %k1 #5.20
vpblendmq %zmm2, %zmm5, %zmm1{%k1} #5.20
movl $240, %eax #5.20
vpblendmq %zmm3, %zmm4, %zmm0{%k1} #5.20
vpblendmq %zmm16, %zmm20, %zmm15{%k1} #5.20
vpblendmq %zmm18, %zmm19, %zmm14{%k1} #5.20
vpermt2q %zmm2, %zmm17, %zmm5 #5.20
vpermt2q %zmm3, %zmm17, %zmm4 #5.20
vpermt2q %zmm16, %zmm17, %zmm20 #5.20
vpermt2q %zmm18, %zmm17, %zmm19 #5.20
valignd $8, %zmm1, %zmm0, %zmm22 #5.20
valignd $8, %zmm5, %zmm4, %zmm24 #5.20
valignd $8, %zmm15, %zmm14, %zmm26 #5.20
valignd $8, %zmm20, %zmm19, %zmm28 #5.20
vmovupd %zmm22, 64(%rdi) #5.7
vmovupd %zmm24, 192(%rdi) #5.7
vmovupd %zmm26, 320(%rdi) #5.7
vmovupd %zmm28, 448(%rdi) #5.7
kmovw %eax, %k2 #5.20
vpblendmq %zmm0, %zmm1, %zmm21{%k2} #5.20
vpblendmq %zmm4, %zmm5, %zmm23{%k2} #5.20
vpblendmq %zmm14, %zmm15, %zmm25{%k2} #5.20
vpblendmq %zmm19, %zmm20, %zmm27{%k2} #5.20
vmovupd %zmm21, (%rdi) #5.7
vmovupd %zmm23, 128(%rdi) #5.7
vmovupd %zmm25, 256(%rdi) #5.7
vmovupd %zmm27, 384(%rdi) #5.7Listing 37: Lines from assembly code for transposition example on Skylake.
2.7. AVX-512F: Gather/Scatter
AVX2 includes a gather operation, which loads vector elements from non-adjacent memory locations into a contiguous 256-bit YMM register. AVX-512F introduces gather with 512-bit registers and also a scatter instruction, which stores elements from a contiguous vector into non-adjacent memory locations.
The listing below shows memory access with non-contiguous memory access, where the code reads a contiguous array Y and scatters its elements into array X with a fixed stride of 8.
void Scatter( double* restrict X, double* restrict Y ) {
int i;
for(i = 0; i < 10000; i++)
X[i*8] = Y[i];
}Listing 38: Scatter example.
In the assembly compiled for Broadwell is shown in the listing below.
..B1.7: # Preds ..B1.7 ..B1.6
# Execution count [1.00e+04]
vmovupd (%rsi,%r8,8), %ymm0 #4.14
movl %r8d, %ecx #4.5
vmovupd 32(%rsi,%r8,8), %ymm2 #4.14
shll $3, %ecx #4.5
addq $8, %r8 #3.3
movslq %ecx, %rcx #4.5
cmpq %rdx, %r8 #3.3
vextractf128 $1, %ymm0, %xmm1 #4.5
vextractf128 $1, %ymm2, %xmm3 #4.5
vmovsd %xmm0, (%rdi,%rcx,8) #4.5
vmovhpd %xmm0, 64(%rdi,%rcx,8) #4.5
vmovsd %xmm1, 128(%rdi,%rcx,8) #4.5
vmovhpd %xmm1, 192(%rdi,%rcx,8) #4.5
vmovsd %xmm2, 256(%rdi,%rcx,8) #4.5
vmovhpd %xmm2, 320(%rdi,%rcx,8) #4.5
vmovsd %xmm3, 384(%rdi,%rcx,8) #4.5
vmovhpd %xmm3, 448(%rdi,%rcx,8) #4.5
jb ..B1.7 # Prob 99% #3.3Listing 39: Lines from the assembly code for the scatter example on Broadwell.
This listing demonstrates that the scatter operation is performed using multiple vextractf128 and scalar vmovsd/vmovhpd instructions. First, vmovupd loads four consecutive values from Y into a YMM register. Then vextractf128 stores half of that YMM register into a new XMM register. vmovsd stores the lower half of the XMM register (which amounts to one 64-bit double precision element) into array X, vmovhpd stores the upper half in the next position in array X. Then the procedure is repeated until all four loaded values are scattered.
The optimization report in the listing below confirms that the loop was vectorized and mentions that a non-unit stride store (i.e., a scatter operation) was emulated for the array A.
LOOP BEGIN at scatter.c(3,3)
remark #15388: vectorization support: reference Y[i] has aligned access [ scatter.c(4,14) ]
remark #15329: vectorization support: non-unit strided store was emulated for the variable <X[i*8]>, stride is 8 [ scatter.c(4,5) ]
remark #15305: vectorization support: vector length 8
remark #15309: vectorization support: normalized vectorization overhead 0.435
remark #15300: LOOP WAS VECTORIZED
remark #15442: entire loop may be executed in remainder
remark #15448: unmasked aligned unit stride loads: 1
remark #15453: unmasked strided stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 5
remark #15477: vector cost: 2.870
remark #15478: estimated potential speedup: 1.730
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=1250
LOOP ENDListing 40: Optimization report for the scatter example on Broadwell.
The code compiled for Skylake (the listing below) shows that the compiler used the instruction vscatterdpd. This instruction belongs to AVX-512F module. It scatters a register of double precision floating-point values to non-contiguous memory locations. The base address is YMM0, the offsets are stored in r9, and the write mask k1/k2 has all bits set to 1.
..B1.7: # Preds ..B1.7 ..B1.6
# Execution count [1.00e+04]
vpcmpeqb %xmm0, %xmm0, %k1 #4.5
movl %r8d, %ecx #4.5
vmovups (%rsi,%r8,8), %zmm1 #4.14
vmovups 64(%rsi,%r8,8), %zmm2 #4.14
shll $3, %ecx #4.5
addq $16, %r8 #3.3
movslq %ecx, %rcx #4.5
lea (%rdi,%rcx,8), %r9 #4.5
vscatterdpd %zmm1, (%r9,%ymm0,8){%k1} #4.5
vpcmpeqb %xmm0, %xmm0, %k2 #4.5
vscatterdpd %zmm2, 512(%r9,%ymm0,8){%k2} #4.5
cmpq %rdx, %r8 #3.3
jb ..B1.7 # Prob 99% #3.3Listing 41: Lines from the assembly code for scatter example on Skylake.
The optimization report in the listing below also shows that the loop was vectorized, but this time non-unit stride store was generated, rather than emulated for access to array A.
LOOP BEGIN at scatter.c(3,3)
remark #15388: vectorization support: reference Y[i] has aligned access [ scatter.c(4,14) ]
remark #15416: vectorization support: non-unit strided store was generated for the variable <X[i*8]>, stride is 8 [ scatter.c(4,5) ]
remark #15305: vectorization support: vector length 16
remark #15309: vectorization support: normalized vectorization overhead 0.270
remark #15300: LOOP WAS VECTORIZED
remark #15442: entire loop may be executed in remainder
remark #15448: unmasked aligned unit stride loads: 1
remark #15453: unmasked strided stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 5
remark #15477: vector cost: 2.310
remark #15478: estimated potential speedup: 2.150
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=625
LOOP ENDListing 42: Optimization report for scatter example on Skylake.
When memory access has good locality, the cost of gather/scatter is high, and the compiler may replace a scatter operation with permutations or shuffles followed by unit-stride access. For example, the code in the listing below accesses memory with a stride of 2. For this pattern, in every cache line, 1 out of 2 elements is written. Stride 2 has better locality than stride 8, where only 1 element out of 8 is written.
void Scatter2( double* restrict X, double* restrict Y ) {
int i;
for(i = 0; i < 10000; i++)
X[i*2] = Y[i];
}Listing 43: Scatter with a small stride example.
AVX-512 assembly for this case is shown in the listing below. Instead of vgatherdpd, the compiler chose to use vexpandpd and vpermpd operations followed by unit-stride masked stores vmovupd.
..B1.7: # Preds ..B1.7 ..B1.6
# Execution count [1.00e+04]
vmovups (%rsi,%r8,8), %zmm2 #4.14
movl %r8d, %ecx #4.5
vmovups 64(%rsi,%r8,8), %zmm5 #4.14
vexpandpd %zmm2, %zmm1{%k1}{z} #4.5
vpermpd %zmm2, %zmm0, %zmm3 #4.5
vexpandpd %zmm5, %zmm4{%k1}{z} #4.5
vpermpd %zmm5, %zmm0, %zmm6 #4.5
addl %ecx, %ecx #4.5
addq $16, %r8 #3.3
movslq %ecx, %rcx #4.5
vmovupd %zmm1, (%rdi,%rcx,8){%k1} #4.5
vmovupd %zmm3, 64(%rdi,%rcx,8){%k1} #4.5
vmovupd %zmm4, 128(%rdi,%rcx,8){%k1} #4.5
vmovupd %zmm6, 192(%rdi,%rcx,8){%k1} #4.5
cmpq %rdx, %r8 #3.3
jb ..B1.7 # Prob 99% #3.3Listing 44: Assembly for the scatter example with a stride of 2 on Skylake.
2.8. AVX-512F: Embedded Broadcasting
Embedded broadcasting, a feature introduced in AVX-512, allows vector instructions to replicate scalar elements across vector lanes and use them as operands. Before AVX-512, broadcasting a scalar across vector lanes was possible, but it required an explicit broadcast operation, and its result occupied an additional vector register. Embedded broadcasting is supported for 32-bit and 64-bit scalars, which get replicated 16 or 8 times, respectively, but not for byte and word types. Because embedded broadcasting does not require an additional register to store the result, it is particularly useful when the register space is in short supply.
The figure below illustrates the difference between broadcast in AVX and AVX-512 for an example kernel A[i]+1.5, where the addition is vectorized in index i.
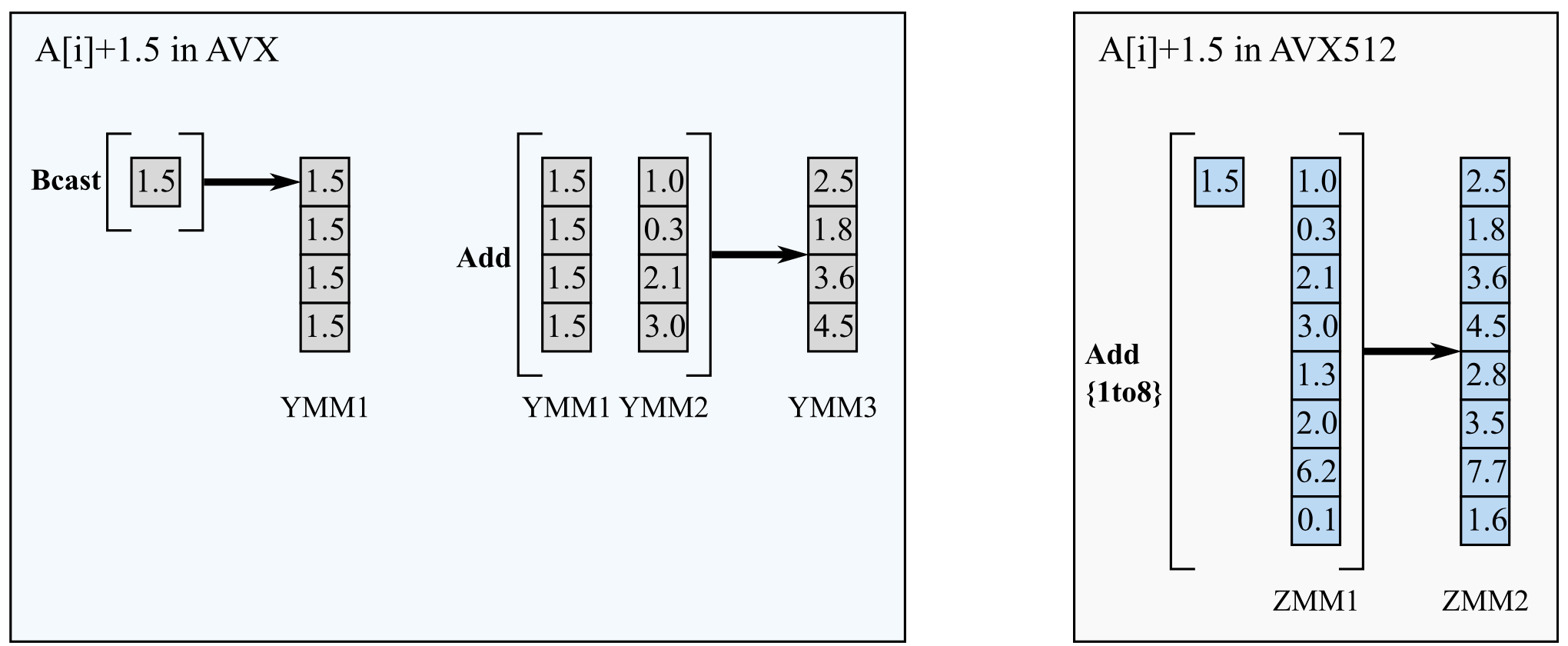
Figure 6: Broadcasting a scalar value across vector lanes in AVX and AVX-512.
The example in the listing below shows a case where embedded broadcasting may be used.
void Embedded_Broadcast (float * restrict A, float * restrict L, float * restrict U) {
int i, j, k;
int n = 16;
for ( i = 0; i < n; i++)
for ( k = 0; k < n; k++)
for ( j = 0; j < n; j++)
A[i*n + j] += L[i*n + k]*U[k*n + j];
}Listing 45: Matrix-matrix multiplication can benefit from embedded broadcast.
In this code, the innermost loop in j gets vectorized. The compiler expresses the multiplication and accumulation operations in the loop for 8 values (in AVX) or 16 values (in AVX-512) of j as an FMA instruction with three operands. Two of these operands are vectors with data loaded from A and U, and the third one has the scalar value L[i*n+k] in all vector lanes.
The listing below shows the assembly for the above example compiled for Broadwell.
..B1.2: # Preds ..B1.2 ..B1.1
# Execution count [4.56e+00]
vmovups 32(%rdi,%rax,4), %ymm4 #8.9
incb %dl #5.3
vmovups (%rdi,%rax,4), %ymm2 #8.9
vbroadcastss 16(%rsi,%rax,4), %ymm3 #8.23
vbroadcastss 12(%rsi,%rax,4), %ymm14 #8.23
vbroadcastss 8(%rsi,%rax,4), %ymm1 #8.23
vbroadcastss 4(%rsi,%rax,4), %ymm13 #8.23
vbroadcastss (%rsi,%rax,4), %ymm15 #8.23
vfmadd231ps -336(%rbp), %ymm3, %ymm4 #8.9[spill]
vfmadd231ps -720(%rbp), %ymm15, %ymm2 #8.9[spill]
vfmadd231ps -400(%rbp), %ymm14, %ymm4 #8.9[spill]
vfmadd231ps -464(%rbp), %ymm1, %ymm4 #8.9[spill]
vfmadd231ps -656(%rbp), %ymm13, %ymm4 #8.9[spill]
...
addq $16, %rax #5.3
cmpb $16, %dl #5.3
jb ..B1.2 # Prob 99% #5.3Listing 46: Lines from the assembly code for matrix multiplication example on Broadwell.
The broadcast operation in this code is separate from the FMA operation. It replicates the value of L[i*n+k] across all vector lanes. The result of the broadcast occupies the register YMM0. This register is subsequently used in the FMA operation, in which the companion operand contains the values of U for 8 values of j.
The potential speedup due to vectorization, according to the optimization report in the listing below, is 5.5 compared to scalar code.
LOOP BEGIN at EB.c(6,5)
remark #15542: loop was not vectorized: inner loop was already vectorized
remark #25436: completely unrolled by 16
LOOP BEGIN at EB.c(7,7)
remark #15389: vectorization support: reference A[i*16+j] has unaligned access [ EB.c(8,9) ]
remark #15389: vectorization support: reference A[i*16+j] has unaligned access [ EB.c(8,9) ]
remark #15389: vectorization support: reference U[k*16+j] has unaligned access [ EB.c(8,34) ]
remark #15381: vectorization support: unaligned access used inside loop body
remark #15305: vectorization support: vector length 8
remark #15427: loop was completely unrolled
remark #15399: vectorization support: unroll factor set to 2
remark #15309: vectorization support: normalized vectorization overhead 0.455
remark #15300: LOOP WAS VECTORIZED
remark #15450: unmasked unaligned unit stride loads: 2
remark #15451: unmasked unaligned unit stride stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 11
remark #15477: vector cost: 1.370
remark #15478: estimated potential speedup: 5.500
remark #15488: --- end vector cost summary ---
LOOP END
LOOP ENDListing 47: Optimization report for matrix multiplication example on Broadwell.
In the case of Skylake, AVX-512 is supported, so the listing below shows embedded broadcast.
..B1.2: # Preds ..B1.2 ..B1.1
vbroadcastss (%rsi,%rax,4), %zmm16 #8.23
incb %dl #5.3
vfmadd213ps (%rdi), %zmm15, %zmm16 #8.9
vfmadd231ps 4(%rsi,%rax,4){1to16}, %zmm14, %zmm16 #8.9
vfmadd231ps 8(%rsi,%rax,4){1to16}, %zmm13, %zmm16 #8.9
vfmadd231ps 12(%rsi,%rax,4){1to16}, %zmm12, %zmm16 #8.9
vfmadd231ps 16(%rsi,%rax,4){1to16}, %zmm11, %zmm16 #8.9
vfmadd231ps 20(%rsi,%rax,4){1to16}, %zmm10, %zmm16 #8.9
vfmadd231ps 24(%rsi,%rax,4){1to16}, %zmm9, %zmm16 #8.9
vfmadd231ps 28(%rsi,%rax,4){1to16}, %zmm8, %zmm16 #8.9
vfmadd231ps 32(%rsi,%rax,4){1to16}, %zmm7, %zmm16 #8.9
vfmadd231ps 36(%rsi,%rax,4){1to16}, %zmm6, %zmm16 #8.9
vfmadd231ps 40(%rsi,%rax,4){1to16}, %zmm5, %zmm16 #8.9
vfmadd231ps 44(%rsi,%rax,4){1to16}, %zmm4, %zmm16 #8.9
vfmadd231ps 48(%rsi,%rax,4){1to16}, %zmm3, %zmm16 #8.9
vfmadd231ps 52(%rsi,%rax,4){1to16}, %zmm2, %zmm16 #8.9
vfmadd231ps 56(%rsi,%rax,4){1to16}, %zmm1, %zmm16 #8.9
vfmadd231ps 60(%rsi,%rax,4){1to16}, %zmm0, %zmm16 #8.9
addq $16, %rax #5.3
vmovups %zmm16, (%rdi) #8.9
addq $64, %rdi #5.3
cmpb $16, %dl #5.3
jb ..B1.2 # Prob 99% #5.3Listing 48: Embedded broadcast in matrix multiplication example on Skylake.
In this assembly, 15 out of 16 broadcast operations are embedded in the vfmadd231ps operation (embedded expressions are the ones with syntax like “4(%rsi,%rax,4){1to16}“). The 16th FMA operation has an implicit load of A from %rdi, which is followed by vfmadd213ps (a different flavor of FMA) to get the correct sequence of arithmetic instructions.
The k-loop is unrolled by 16, and the code uses a total of 16+1=17 registers: ZMM0 … ZMM15 containing matrix U and register ZMM16 containing the destination A. If embedded broadcasting was not available, the compiler would have had to implement explicit broadcasts, and we would need additional 16 registers for a total of 17+16=33 registers. This is too many to fit in the AVX-512 register file. Therefore, the unroll factor would have to be reduced, leading to sub-optimal performance.
The optimization report for Skylake in the listing below shows the estimated potential speedup of 8.38.
LOOP BEGIN at EB.c(6,5)
remark #15542: loop was not vectorized: inner loop was already vectorized
remark #25436: completely unrolled by 16
LOOP BEGIN at EB.c(7,7)
remark #15300: LOOP WAS VECTORIZED
remark #15450: unmasked unaligned unit stride loads: 2
remark #15451: unmasked unaligned unit stride stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 11
remark #15477: vector cost: 0.680
remark #15478: estimated potential speedup: 8.380
remark #15488: --- end vector cost summary ---
LOOP END
LOOP ENDListing 49: Optimization report for matrix multiplication example on Skylake.
2.9. AVX-512F: Ternary Logic
A new operation, ternary logic, is introduced by AVX-512F to execute any bitwise logical functions on three operands in one instruction. The ternary logic instruction accepts three short vector arguments, up to 512-bits each, and an 8-bit integer representing an arbitrary truth table. To apply the logical function with this truth table to the input data, the processor traverses the three input vectors bit by bit. Each triplet of bits forms an index, which is then used to look up the output bit in the truth table.
The application of the ternary logic function is shown in the figure below.
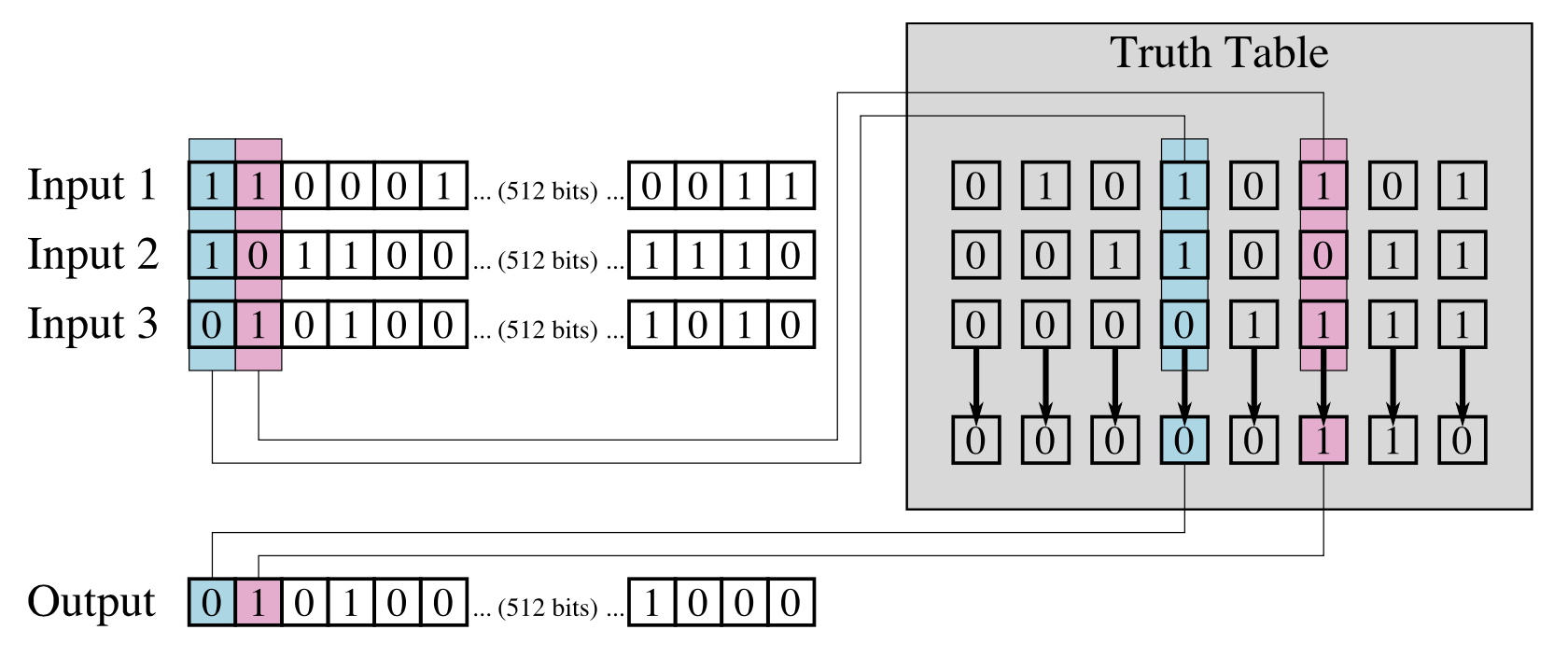
Figure 7: Ternary logic in AVX-512.
The example in the listing below performs a ternary operation with bitwise OR and bitwise AND operators.
void Ternary_Logic (int * restrict A, int * restrict B, int * restrict C) {
int i, n;
#pragma vector aligned
#pragma nounroll
for (i = 0; i < n; i++) {
A[i]= B[i] ^ A[i] & C[i];
}
}Listing 50: Bitwise logic instruction example.
In the code for Broadwell shown in the listing below, the AND and XOR are issued separately.
..B1.8: # Preds ..B1.8 ..B1.7
# Execution count [5.00e+00]
vmovdqu (%rdi,%rcx,4), %ymm0 #6.18
vpand (%rdx,%rcx,4), %ymm0, %ymm1 #6.25
vpxor (%r8,%rcx,4), %ymm1, %ymm2 #6.25
vmovdqu %ymm2, (%rdi,%rcx,4) #6.5
addq $8, %rcx #5.3
cmpq %rax, %rcx #5.3
jb ..B1.8 # Prob 82% #5.3 Listing 51: Lines from the assembly code for bitwise logic instruction example on Broadwell.
The optimization report shown in the listing below shows an estimated potential speedup of 9.150.
LOOP BEGIN at TR.c(5,3)
... vectorization support: reference A[i] has aligned access [ TR.c(6,5) ]
... vectorization support: reference B[i] has aligned access [ TR.c(6,11) ]
... vectorization support: reference A[i] has aligned access [ TR.c(6,18) ]
... vectorization support: reference C[i] has aligned access [ TR.c(6,25) ]
... vectorization support: vector length 8
... LOOP WAS VECTORIZED
... unmasked aligned unit stride loads: 3
... unmasked aligned unit stride stores: 1
... --- begin vector cost summary ---
... scalar cost: 9
... vector cost: 0.870
... estimated potential speedup: 9.150
... --- end vector cost summary ---
LOOP ENDListing 52: Optimization report for bitwise logic instruction example on Broadwell.
In the code compiled for Skylake with AVX-512, the vpternlogd instruction is used to perform both AND and XOR logical operations in one instruction.
..B1.8: # Preds ..B1.8 ..B1.7
# Execution count [5.00e+00]
vmovups (%rax,%rsi,4), %zmm1 #6.11
vmovups (%r9,%rsi,4), %zmm0 #6.18
vpternlogd $120, (%rdx,%rsi,4), %zmm0, %zmm1 #6.25
vmovdqu32 %zmm1, (%r9,%rsi,4) #6.5
addq $16, %rsi #5.3
cmpq %rcx, %rsi #5.3
jb ..B1.8 # Prob 82% #5.3Listing 53: Lines from the assembly code for bitwise logic instruction example on Skylake.
According to the optimization report in the listing below, the estimated potential speedup due to vectorization and, consequently, due to the ternary logic function, is 19.280.
LOOP BEGIN at TR.c(5,3)
... vectorization support: reference A[i] has aligned access [ TR.c(6,5) ]
... vectorization support: reference B[i] has aligned access [ TR.c(6,11) ]
... vectorization support: reference A[i] has aligned access [ TR.c(6,18) ]
... vectorization support: reference C[i] has aligned access [ TR.c(6,25) ]
... vectorization support: vector length 16
... LOOP WAS VECTORIZED
... unmasked aligned unit stride loads: 3
... unmasked aligned unit stride stores: 1
... --- begin vector cost summary ---
... scalar cost: 9
... vector cost: 0.430
... estimated potential speedup: 19.280
... --- end vector cost summary ---
LOOP ENDListing 54: Optimization report for bitwise logic instruction example on Skylake.
2.10. AVX-512F: Embedded Rounding
Intel AVX-512 introduces the embedded rounding feature, which allows most arithmetic instructions to define a rounding mode applied to just this particular instruction. To take advantage of this feature, instructions must use a rounding attribute. Embedded rounding overrides the rounding mode set by the control register MXCSR. In addition to the rounding mode, AVX-512 instructions support embedded suppression of exceptions.
While it is not possible to set embedded rounding in automatically vectorized code, the user can control rounding at instruction level with the help of intrinsic functions that have the suffix _round_. The listing below shows an example of this functionality.
#include <immintrin.h>
void DivRound(float *A, float *B, float *C) {
for (int i = 0; i < 1024; i += 16) {
__m512 A_vec = _mm512_load_ps(A + i);
__m512 B_vec = _mm512_load_ps(B + i);
__m512 C_vec = _mm512_div_round_ps(A_vec, B_vec, _MM_FROUND_TO_NEAREST_INT | _MM_FROUND_NO_EXC);
_mm512_store_ps(C + i, C_vec);
}
}Listing 55: Example: vector division with embedded rounding using intrinsics.
Our intrinsics-based example code results in the assembly shown in the listing below.
..B1.2: # Preds ..B1.2 ..B1.1
# Execution count [6.25e+01]
vmovups (%rdi,%rax,4), %zmm0 #7.20
vmovups (%rsi,%rax,4), %zmm1 #7.20
vdivps {rn-sae}, %zmm1, %zmm0, %zmm2 #7.20
vmovups %zmm2, (%rdx,%rax,4) #8.21
addq $16, %rax #4.29
cmpq $1024, %rax #4.23
jl ..B1.2 # Prob 98% #4.23Listing 56: Compiled division with embedded rounding.
Here the attribute rn of the vdivps instruction indicates the rounding mode of the vector division operation, rounding to the nearest integer. The sae part of the attribute instructs the processor to suppress all floating-point exceptions.
Other rounding modes supported in AVX-512 are shown in the table below.
| Flag | Setting |
|---|---|
| _MM_FROUND_TO_NEAREST_INT | round to nearest integer |
| _MM_FROUND_TO_NEG_INF | round down toward -∞ |
| _MM_FROUND_TO_POS_INF | round up toward +∞ |
| _MM_FROUND_TO_ZERO | truncate |
| _MM_FROUND_NO_EXC | (in combination with the above) suppress floating-point exceptions |
Table 3: Rounding modes in AVX-512.
3. Skylake and Knights Landing
In this section, we discuss the main differences between AVX-512 on Skylake and Knights Landing. As we mentioned in Section 1.1, the first two processors to support Intel AVX-512 instructions are Intel Xeon Phi processor family x200 (2016, formerly Knights Landing) and Intel Xeon processor Scalable family (2017, formerly Skylake).
However, the modules of AVX-512 used in these architectures are different. Knights Landing supports AVX-512F, AVX-512CD, AVX-512ER, and AVX-512PF. Skylake supports AVX-512F, AVX-512CD, AVX-512VL, AVX-512BW, and AVX-512DQ.
3.1. AVX-512ER: Exponential, Reciprocal
AVX-512ER, the “exponential and reciprocal” module, provides high-accuracy base-2 exponential, reciprocal and reciprocal square root instructions. It is supported by KNL only. The base-2 exponential function in AVX-512ER provides a maximum relative error of 2-23, and the reciprocal and reciprocal square root provide an error of 2-28. These high-accuracy functions are an improvement over the functionality of AVX-512F, in which the exponential function is not supported, and the reciprocal and reciprocal square root functions provide a maximum relative error of 2-14.
In automatically vectorized codes, access to the AVX-512ER instructions in double precision is provided via the Math library SIMD-enabled functions exp2(x) and invsqrt(x) and the division operator 1.0/x. In single precision, the functions are exp2f(x) and invsqrtf(x), and the operator is 1.0f/x. Intel compilers may translate these functions to vector code in different ways, depending on whether AVX-512ER is available in the target architecture, and depending on the required transcendental function accuracy. The required accuracy can be set, for example, with the argument -fimf-precision=low|medium|high or -fimf-accuracy-bits=n. Specifically, the Math library function call may be translated into one of the following in the assembly:
- the corresponding AVX-512F or AVX-512ER vector instruction combined with a normalization of the function argument,
- the corresponding AVX-512F or AVX-512ER vector instruction followed by Newton-Raphson iteration to improve accuracy,
- a polynomial approximation to the function with a normalized argument, or
- a call to an SVML (Short Vector Math Library) function implementing an analytic approximation of the transcendental function.
The specific recommendations for implementation can be found in Section 13.24 of the Intel® 64 and IA-32 Architectures Optimization Reference Manual.
Additionally, in the table below we show the implementation of the three functions in single precision and in double precision for Skylake and Knights Landing produced by the Intel C compiler 17.0.2.174. We compiled the code with -fimf-precision=low to obtain the low-accuracy implementation and -fimf-precision=high for the high-accuracy one.
| High Accuracy | Low Accuracy | |||
|---|---|---|---|---|
| Skylake | Knights Landing | Skylake | Knights Landing | |
| exp2(x) | svml_exp28_ha | svml_exp28_ha | svml_exp28_ep | svml_exp28_ep |
| exp2f(x) | svml_exp2f16_ha | svml_exp2f16_ha | Polynomial | vexp2ps |
| invsqrt(x) | svml_invsqrt8_ha | vrsqrt28pd + NR | svml_invsqrt8_ep | vrsqrt28pd |
| invsqrtf(x) | svml_invsqrtf16_ha | vrsqrt28ps | svml_invsqrtf16_ep | svml_invsqrtf16_ha |
| 1.0/x | vdivpd | vdivpd | vdivpd | vrcp28pd + NR |
| 1.0f/x | vdivps | vdivps | vrcp14ps + NR | vrcp14ps |
Table 4: Implementation of transcendental math in vector calculations.
To give you a better idea of how the various implementations look in code, we compiled the example in the listing below for the reciprocal square root operation for both architectures: Skylake and Knights Landing.
void Reciprocal_sqrt (double * restrict A, double * restrict B) {
int i;
for ( i = 0; i < 10000; i++)
B[i] = invsqrt(A[i]);
}Listing 57: Reciprocal square root example .
First, we compiled the code for Skylake with -xCORE-AVX512 and -fimf-precision=high and obtained the assembly shown in the listing below.
vmovups (%r14,%r13,8), %zmm0 #4.20
vmovups 64(%r14,%r13,8), %zmm16 #4.20
call __svml_invsqrt8_ha #4.12
vmovaps %zmm0, %zmm17 #4.12
vmovaps %zmm16, %zmm0 #4.12
call __svml_invsqrt8_ha #4.12
vmovupd %zmm17, (%rsi,%r13,8) #4.5
vmovupd %zmm0, 64(%rsi,%r13,8) #4.5Listing 58: Lines from assembly code for reciprocal square root operation with high accuracy for Skylake.
This code relies on the high-accuracy implementation (see suffix _ha) of the reciprocal square root from the SVML.
Second, we recompiled the code for Knights Landing with -xMIC-AVX512, still keeping the precision flag -fimf-precision=high. This resulted in the assembly shown in the listing below.
vmovups (%rdi,%r8,8), %zmm5 #4.20 c1
vmovups 64(%rdi,%r8,8), %zmm10 #4.20 c1
vmovaps %zmm4, %zmm2 #4.12 c1
vmovaps %zmm4, %zmm8 #4.12 c1
vpcmpq $1, .L_2il0floatpacket.2(%rip){1to8}, %zmm5, %k1 #4.12 c7 stall 2
vpcmpq $1, .L_2il0floatpacket.2(%rip){1to8}, %zmm10, %k2 #4.12 c7
vscalefpd .L_2il0floatpacket.3(%rip){1to8}, %zmm5, %zmm5{%k1} #4.12 c9
vscalefpd .L_2il0floatpacket.3(%rip){1to8}, %zmm10, %zmm10{%k2} #4.12 c9
vrsqrt28pd %zmm5, %zmm0 #4.12 c11
vrsqrt28pd %zmm10, %zmm6 #4.12 c11
vpandq .L_2il0floatpacket.4(%rip){1to8}, %zmm0, %zmm11 #4.12 c19 stall 3
vpandq .L_2il0floatpacket.4(%rip){1to8}, %zmm6, %zmm12 #4.12 c19
vmulpd {rn-sae}, %zmm11, %zmm11, %zmm1 #4.12 c21
vmulpd {rn-sae}, %zmm12, %zmm12, %zmm7 #4.12 c21
vfnmadd213pd .L_2il0floatpacket.5(%rip){1to8}, %zmm5, %zmm1 #4.12 c27 stall 2
vfnmadd213pd .L_2il0floatpacket.5(%rip){1to8}, %zmm10, %zmm7 #4.12 c27
vfmadd213pd .L_2il0floatpacket.2(%rip){1to8}, %zmm1, %zmm2 #4.12 c33 stall 2
vfmadd213pd .L_2il0floatpacket.2(%rip){1to8}, %zmm7, %zmm8 #4.12 c33
vmulpd {rn-sae}, %zmm2, %zmm1, %zmm3 #4.12 c39 stall 2
vmulpd {rn-sae}, %zmm8, %zmm7, %zmm9 #4.12 c39
vfmadd231pd %zmm11, %zmm3, %zmm11 #4.12 c45 stall 2
vfmadd231pd %zmm12, %zmm9, %zmm12 #4.12 c45
vscalefpd .L_2il0floatpacket.7(%rip){1to8}, %zmm11, %zmm11{%k1} #4.12 c51 stall 2
vscalefpd .L_2il0floatpacket.7(%rip){1to8}, %zmm12, %zmm12{%k2} #4.12 c51
vfixupimmpd $112, .L_2il0floatpacket.8(%rip){1to8}, %zmm5, %zmm11 #4.12 c53
vmovupd %zmm11, (%rsi,%r8,8) #4.5 c55
vfixupimmpd $112, .L_2il0floatpacket.8(%rip){1to8}, %zmm10, %zmm12 #4.12 c55
vmovupd %zmm12, 64(%rsi,%r8,8) #4.5 c57Listing 59: Reciprocal square root in double precision with high accuracy on Knights Landing.
Here the compiler used the AVX-512ER instruction vrsqrt28pd followed by Newton-Raphson iterations to improve accuracy.
Finally, we compiled the code for Skylake with -fimf-precision=low. The result is shown in the listing below.
vmovups (%rdi,%r8,8), %zmm0 #4.20 c1
vmovups 64(%rdi,%r8,8), %zmm1 #4.20 c1
vpcmpq $1, .L_2il0floatpacket.2(%rip){1to8}, %zmm0, %k1 #4.12 c7 stall 2
vpcmpq $1, .L_2il0floatpacket.2(%rip){1to8}, %zmm1, %k2 #4.12 c7
vscalefpd .L_2il0floatpacket.3(%rip){1to8}, %zmm0, %zmm0{%k1} #4.12 c9
vscalefpd .L_2il0floatpacket.3(%rip){1to8}, %zmm1, %zmm1{%k2} #4.12 c9
vrsqrt28pd %zmm0, %zmm2 #4.12 c11
vrsqrt28pd %zmm1, %zmm3 #4.12 c11
vscalefpd .L_2il0floatpacket.4(%rip){1to8}, %zmm2, %zmm2{%k1} #4.12 c19 stall 3
vmovupd %zmm2, (%rsi,%r8,8) #4.5 c21
vscalefpd .L_2il0floatpacket.4(%rip){1to8}, %zmm3, %zmm3{%k2} #4.12 c21
vmovupd %zmm3, 64(%rsi,%r8,8) #4.5 c23Listing 60: Reciprocal square root in double precision with low accuracy on Knights Landing.
Here the compiler only normalizes the argument of the reciprocal square root and then uses vrsqrt28pd without Newton-Raphson iterations.
3.2. AVX-512PF: Prefetch for Gather/Scatter
AVX-512PF is an AVX-512 module featuring the “Prefetch” instructions for gather and scatter operations. This module is included in the Knights Landing architecture, but not in Skylake. The instructions of AVX-512PF allow the code to prefetch 8 or 16 elements into the L1 or the L2 cache. The element addresses are specified in the instruction with a base address and a vector of 32-bit or 64-bit offsets. These instructions are useful for codes with complex memory access patterns where the automatic hardware prefetching functionality is not sufficient.
Prefetching is not unique to AVX-512PF. Indeed, it is also available in SSE, where the prefetchnta, prefetcht0, prefetcht1, and prefetcht2 can be used to prefetch a cache line from memory into the L1 or L2 cache before the core needs it. This strategy can reduce the latency of memory accesses by partially overlapping data movement with computation. In each architecture, there is a limit on how many prefetch instructions can be executed concurrently per core. This limit together with the latency of memory access determines the maximum achievable memory bandwidth.
It is not necessary to use software prefetching to achieve a high bandwidth of memory access. That is because most Intel architecture processors also have hardware prefetching, which is applied to the running code automatically. When the memory access pattern is predictable, the hardware prefetch unit in the core trains on the pattern and sets the hardware prefetch distance automatically.
What makes the AVX-512PF prefetch different from the SSE prefetch instruction is that the AVX-512PF prefetch requires just one instruction to fetch up to 16 elements scattered in memory, while the SSE prefetch accesses only a single cache line, i.e., 64 consecutive bytes.
An example of code with memory access pattern that calls for automatic prefetching with AVX-512PF is shown in the listing below.
void Transpose(float* restrict dest, float* restrict source, int* restrict offset, int n) {
int i;
for (i = 0; i < n; i++)
dest[i] = source[offset[i]];
}Listing 61: Code with indirect memory access may be optimized with software prefetching.
In this code, the array source can be prefetched with the AVX-512PF instruction, which will gather 16 values pointed to by the indices in offset before these values are used to write into dist.
Without AVX-512PF (e.g., on Skylake), prefetching is still possible, but with the help of as many as 16 regular prefetch instructions, each of which prefetches a cache line containing one element of source. To observe this, we compiled this code for the Skylake architecture as shown in the listing below. To illustrate the handling of prefetching and AVX2 gather instruction, we used -vec-threshold0 to force vectorization with the gather instruction even though the compiler estimated that vectorization was not profitable in this case.
icc -xCORE-AVX512 -O3 -qopt-prefetch=5 -vec-threshold0 -S -qopt-report-embed indirect.c Listing 62: Compilation for Skylake with automatic prefetching.
The resulting assembly is shown in the listing below.
..B1.13: # Preds ..B1.15 ..B1.12
vmovups (%r9,%rcx), %zmm0 #4.22
vpcmpeqb %xmm0, %xmm0, %k1 #4.15
vpxord %zmm1, %zmm1, %zmm1 #4.15
vgatherdps (%rsi,%zmm0,4), %zmm1{%k1} #4.15
vmovups %zmm1, (%r9,%rdi) #4.5
cmpl %r8d, %r10d #3.3
jg ..B1.15 # Prob 18% #3.3
..B1.14: # Preds ..B1.13
movslq 128(%r9,%rcx), %r11 #4.22
prefetcht1 (%rsi,%r11,4) #4.15
movslq (%rcx), %r11 #4.22
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht1 (%rsi,%r11,4) #4.15
prefetcht0 512(%r9,%rcx) #4.22
prefetcht0 512(%r9,%rdi) #4.5
..B1.15: # Preds ..B1.13 ..B1.14
addl $16, %edx #3.3
addq $64, %r9 #3.3
addl $16, %r10d #3.3
cmpl %r8d, %edx #3.3
jb ..B1.13 # Prob 82% #3.3Listing 63: Gather with prefetching for Skylake.
The long list of prefetcht1 instructions fetches 16 elements from RAM to the level 2 cache for a subsequent vgatherdps operation.
In contrast, when we compile for Knights Landing as shown in the listing below, we see a different result.
icc -xMIC-AVX512 -O3 -qopt-prefetch=5 -S -qopt-report-embed indirect.c Listing 64: Compilation with automatic prefetching.
The assembly produced by the above compilation command is shown in the listing below.
..B1.12: # Preds ..B1.14 ..B1.11
# Execution count [5.00e+00]
vmovups (%r9,%r8), %zmm0 #6.22 c1
vpxord %zmm1, %zmm1, %zmm1 #6.15 c1
kmovw %k1, %k2 #6.15 c1
vgatherdps (%rsi,%zmm0,4), %zmm1{%k2} #6.15 c7 stall 2
vmovups %zmm1, (%r9,%rdi) #6.5 c13 stall 2
cmpl %edx, %r10d #5.3 c13
jg ..B1.14 # Prob 18% #5.3 c15
# LOE rbx rbp rsi rdi r8 r9 r12 r13 r14 r15 eax edx ecx r10d k1
..B1.13: # Preds ..B1.12
# Execution count [4.10e+00]
prefetcht0 512(%r9,%r8) #6.22 c1
vpbroadcastd 512(%r9,%r8), %zmm0 #6.15 c1
vgatherpf1dps (%rsi,%zmm0){%k1} #6.15 c7 stall 2
prefetcht0 512(%r9,%rdi) #6.5 c7
# LOE rbx rbp rsi rdi r8 r9 r12 r13 r14 r15 eax edx ecx r10d k1
..B1.14: # Preds ..B1.12 ..B1.13
# Execution count [5.00e+00]
addl $16, %eax #5.3 c1
addq $64, %r9 #5.3 c1
addl $16, %r10d #5.3 c3
cmpl %edx, %eax #5.3 c3
jb ..B1.12 # Prob 82% #5.3 c5Listing 65: Gather with prefetching for Knights Landing.
Instead of 16 prefetch instructions, there is a single vgatherpd1dps instruction for access to array source. Arrays dest and offset are accessed with unit stride (i.e., consecutively), so for these arrays, the compiler inserted the regular SSE prefetcht0 instructions.
To enable automatic generation of AVX-512PF prefetch instructions by Intel compilers, use the optimization level -O3 and the argument -qopt-prefetch=5 like we did above. Additional fine-tuning of AVX-512PF instructions is possible only via the intrinsic function _mm512_i32_gather_ps() and other variants of this intrinsic (masked, scatter, double precision and 64-bit index intrinsics).
If you want to tune regular prefetching (i.e., SSE cache line prefetch), then additional fine-tuning is also available with one of the following methods. None of the methods listed below result in AVX-512PF; the only access to AVX-512PF is through the above-mentioned intrinsics and automatic vectorization.
-
- You can place directive #pragma prefetch before a loop (similar syntax available in Fortran), which specifies the prefetched variable, distance and the prefetch hint (i.e., destination cache). For example, the code shown below prefetches array source into the L1 cache with a distance of 8 iterations. This directive requires the compiler argument -qopt-prefetch=n with n at least 2.
#include <immintrin.h>
...
#pragma prefetch source:_MM_HINT_T0:8
for (i = 0; i < n; i++)
dest[i] = source[offset[i]];- Use the compiler argument -qopt-prefetch-distance=n1[,n2] combined with -qopt-prefetch-distance=5 to request a prefetch distance of n1 for the L2 cache and, optionally, a distance of n2 for prefetching to the L1 cache.
- Insert the intrinsic _mm_prefetch() in the code.
3.3. AVX-512DQ: Double and Quad Words
AVX-512DQ is a module of AVX-512 supported by Skylake to extend the support for double word (i.e., 32-bit) and quadword (64-bit) types for some of the operations available in AVX-512F. For instance, AVX-512DQ includes:
- instructions for converting 32- and 64-bit floating-point numbers to 64-bit integers,
- instructions for converting 64-bit integers to 32- and 64-bit floating-point numbers,
- multiplication of 64-bit integers with intermediate results stored as 128-bit integers,
- reduction operations (min, max, sum) across vectors of 32- and 64-bit floating-point numbers.
AVX-512DQ is not available in the Knights Landing architecture.
The listing below shows an example for conversion from double precision floating-point elements to 64-bit integers.
void Convert (long * restrict A, double * restrict B) {
int i;
for ( i = 0; i < 10000; i++)
A[i]=(long)B[i];
}Listing 66: Conversion example: 64-bit floating-point numbers to 64-bit integers.
For the Skylake target (i.e., with the compiler argument -xCORE-AVX512), the compiler-generated assembly looks like in the listing below.
..B1.8: # Preds ..B1.8 ..B1.7
vcvttpd2qq (%rsi,%r8,8), %zmm0 #5.16
vcvttpd2qq 64(%rsi,%r8,8), %zmm1 #5.16
vcvttpd2qq 128(%rsi,%r8,8), %zmm2 #5.16
vcvttpd2qq 192(%rsi,%r8,8), %zmm3 #5.16
vmovdqu64 %zmm0, (%rdi,%r8,8) #5.5
vmovdqu64 %zmm1, 64(%rdi,%r8,8) #5.5
vmovdqu64 %zmm2, 128(%rdi,%r8,8) #5.5
vmovdqu64 %zmm3, 192(%rdi,%r8,8) #5.5
addq $32, %r8 #4.3
cmpq %rdx, %r8 #4.3
jb ..B1.8 # Prob 99% #4.3Listing 67: Lines from assembly code for conversion example on Skylake.
Here the instruction vcvttpd2qq is used for the conversion operation on ZMM registers. This instruction belongs to AVX-512DQ module, and it converts 64-bit floating-point numbers to 64-bit integers with truncation.
LOOP BEGIN at convert.c(4,3)
remark #15300: LOOP WAS VECTORIZED
remark #15442: entire loop may be executed in remainder
remark #15449: unmasked aligned unit stride stores: 1
remark #15450: unmasked unaligned unit stride loads: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 7
remark #15477: vector cost: 0.560
remark #15478: estimated potential speedup: 12.350
remark #15487: type converts: 1
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=312
LOOP ENDListing 68: Optimization report for conversion example on Skylake.
In the case of the Knights Landing target (-xMIC-AVX512), the listing below shows the assembly produced by the compiler. In this case, instruction vcvttsd2si was used, which belongs to the AVX-512F module. It converts the floating-point number contained in the lower 64 bits of the XMM register to a 64-bit integer with truncation.
..B1.8: # Preds ..B1.8 ..B1.7
vmovups (%rsi,%rcx,8), %zmm10 #5.16 c1
vmovups 64(%rsi,%rcx,8), %zmm6 #5.16 c1
vpermpd %zmm10, %zmm13, %zmm2 #5.16 c7 stall 2
vpermpd %zmm10, %zmm16, %zmm5 #5.16 c7
vpermpd %zmm10, %zmm11, %zmm7 #5.16 c9
vcvttsd2si %xmm2, %r12 #5.16 c11
movq %r12, 96(%rsp) #5.16 c13
vpermpd %zmm6, %zmm16, %zmm2 #5.16 c13
vcvttsd2si %xmm5, %r9 #5.16 c15
movq %r9, 72(%rsp) #5.16 c17
...
addq $32, %rcx #4.3 c111
cmpq %rax, %rcx #4.3 c113
jb ..B1.8 # Prob 99% #4.3 c115Listing 69: Lines from assembly code for conversion example on Knights landing.
LOOP BEGIN at convert.c(4,3)
remark #15300: LOOP WAS VECTORIZED
remark #15442: entire loop may be executed in remainder
remark #15449: unmasked aligned unit stride stores: 1
remark #15450: unmasked unaligned unit stride loads: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 7
remark #15477: vector cost: 0.560
remark #15478: estimated potential speedup: 12.350
remark #15487: type converts: 1
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=312
LOOP ENDListing 70: Optimization report for conversion example on Knights landing.
3.4. AVX-512BW: Byte and Word Support
The AVX-512BW module available in Skylake offers basic arithmetic operations and masking for 512-bit vectors of byte-size (8-bit) and word-size (16-bit) integer elements. A processor with AVX-512BW can perform plain or masked addition, multiplication, comparison, element broadcast, type conversion, permutation, min/max reduction and bitwise operations on vectors of 64 elements of byte size or 32 elements of word size.
This functionality is useful for applications with byte- or word-size data elements, including image processing and experimental data analysis.
In Knights Landing, where AVX-512BW is not available, such data would require conversion to 32-bit elements for processing with 512-bit vectors. Alternatively, KNL can perform 8-bit and 16-bit arithmetics with legacy 256-bit AVX2 instructions. In contrast, Skylake can do data storage and arithmetic on 8-bit or 16-bit elements using the full 512-bit vector width.
The listing below shows an example requiring byte-size element support. The directive #pragma vector aligned promises to the compiler that both A and B begin on a 64-byte aligned boundary. At the time of allocation of these arrays, this alignment must be enforced for the code to work correctly.
void Byte_Add (char * restrict A, char * restrict B) {
int i;
#pragma vector aligned
for ( i = 0; i < 10000; i++)
if(A[i]>1)
A[i]=B[i]+1;
}Listing 71: Byte-word support example: operations on 8-bit integers.
In the case of Skylake, the assembly in the listing below shows that the vpcmpgtb instruction operating on ZMM registers was used. This instruction compares packed 8-bit signed integers in ZMM registers and sets a vector mask to reflect zero/non-zero status for each element of the result. After that, masked vpaddb is used for addition of byte-size elements in 512-bit ZMM resisters. Arithmetic in ZMM was possible because of the AVX-512BW module.
..B1.2: # Preds ..B1.2 ..B1.1
vmovups (%rax,%rdi), %zmm1 #7.7
vmovups 64(%rax,%rdi), %zmm2 #7.7
vpcmpgtb %zmm0, %zmm1, %k1 #6.13
vpcmpgtb %zmm0, %zmm2, %k2 #6.13
vpaddb (%rsi,%rax), %zmm0, %zmm1{%k1} #7.17
vpaddb 64(%rsi,%rax), %zmm0, %zmm2{%k2} #7.17
vmovdqu32 %zmm1, (%rax,%rdi) #7.7
vmovdqu32 %zmm2, 64(%rax,%rdi) #7.7
addq $128, %rax #5.3
cmpq $9984, %rax #5.3
jb ..B1.2 # Prob 99% #5.3Listing 72: Lines from assembly code for byte-word support example on Skylake.
The optimization report in the listing below shows an estimated speedup of 52.740.
LOOP BEGIN at bw.c(5,3)
...
remark #15305: vectorization support: vector length 64
remark #15399: vectorization support: unroll factor set to 2
remark #15300: LOOP WAS VECTORIZED
...
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 15
remark #15477: vector cost: 0.280
remark #15478: estimated potential speedup: 52.740
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=78
LOOP ENDListing 73: Optimization report for byte-word support example on Skylake.
In the case of Knights Landing, assembly code in the listing below shows that the vpcmpgtb instruction is used, but this time it is a part of the AVX2 instruction set, which operates on YMM registers. The compiler did not use AVX-512 instructions to vectorize these operations on 8-bit integers because the minimum element size in AVX-512F is 32 bits, and Knights Landing does not support AVX-512BW.
..B1.2: # Preds ..B1.2 ..B1.1
vmovdqu (%rax,%rdi), %ymm1 #7.7 c1
vmovdqu 32(%rax,%rdi), %ymm5 #7.7 c1
vpcmpgtb %ymm0, %ymm1, %ymm3 #6.13 c7 stall 2
vpaddb (%rsi,%rax), %ymm0, %ymm2 #7.7 c7
vpcmpgtb %ymm0, %ymm5, %ymm7 #6.13 c7
vpaddb 32(%rsi,%rax), %ymm0, %ymm6 #7.7 c7
vpblendvb %ymm3, %ymm2, %ymm1, %ymm4 #7.7 c9
vmovdqu %ymm4, (%rax,%rdi) #7.7 c11
vpblendvb %ymm7, %ymm6, %ymm5, %ymm8 #7.7 c11
vmovdqu %ymm8, 32(%rax,%rdi) #7.7 c13
addq $64, %rax #5.3 c13
cmpq $9984, %rax #5.3 c15
jb ..B1.2 # Prob 99% #5.3 c17Listing 74: Lines from assembly code for byte-word support example on Knights landing.
According to the optimization report in the listing below, the use of YMM decreases the vector length to 32 and reduces the estimated speedup due to vectorization from 52.740 to 26.530.
LOOP BEGIN at bw.c(5,3)
...
remark #15305: vectorization support: vector length 32
remark #15399: vectorization support: unroll factor set to 2
remark #15300: LOOP WAS VECTORIZED
...
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 15
remark #15477: vector cost: 0.560
remark #15478: estimated potential speedup: 26.530
remark #15488: --- end vector cost summary ---
remark #25015: Estimate of max trip count of loop=156
LOOP ENDListing 75: Optimization report for byte-word support example on Knights landing.
3.5. AVX-512VL: Vector Length Orthogonality
The AVX-512VL feature available in the Skylake architecture allows most of the AVX-512 instructions to operate at three vector lengths: 128-bit (XMM), 256-bit (YMM) and 512-bit (ZMM). The suffix -VL denotes the full name of this feature, “Vector Length Orthogonality”. This feature allows AVX-512 instructions to operate on XMM or YMM registers, which are normally used in SSE and AVX, respectively, and at the same time use the AVX-512 capabilities, including 32 vector registers and 8 opmask registers. AVX-512VL is important for applications in which the amount of data parallelism cannot fill the 512-bit vector register. It is not possible to use embedded rounding in instructions that rely on AVX-512VL. In Knights Landing, the AVX-512VL feature is not available.
The listing below shows an example where vector length orthogonality can be useful.
void bitwise_op (char * restrict A, char * restrict B, char * restrict C) {
int i;
for ( i = 0; i < 16; i++)
B[i] = A[i] & B[i] | C[i];
}Listing 76: Vector length support example: a ternary bitwise operation on 16-byte vectors.
This workload uses two bitwise logical operations, and as we know from Section 2.9, AVX-512 can process it as a ternary operation. However, with only 16 bytes of data processed in the loop, the 64-byte ZMM registers will not be filled. At the same time, it is not possible to use SSE instructions on 16-byte XMM registers, either, because ternary operations are not available on SSE.
In the case of Skylake, the assembly in the listing below shows that the ternary instruction vpternlogd is used to perform bitwise logical operations on three operands. This instruction belongs to AVX-512F and supported by AVX-512VL so it can operate on the lower 128 bits of the ZMM registers named as XMM registers.
vmovdqu (%rdi), %xmm0 #5.14
vmovdqu (%rdx), %xmm1 #5.28
vpternlogd $248, (%rsi), %xmm0, %xmm1 #5.28
vmovdqu %xmm1, (%rsi) #5.7
ret #6.1Listing 77: Lines from assembly code for vector length support example on Skylake.
LOOP BEGIN at VL.c(4,3)
remark #15300: LOOP WAS VECTORIZED
remark #15450: unmasked unaligned unit stride loads: 3
remark #15451: unmasked unaligned unit stride stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 13
remark #15477: vector cost: 1.000
remark #15478: estimated potential speedup: 7.420
remark #15488: --- end vector cost summary ---
LOOP ENDListing 78: Optimization report for vector length support example on Skylake.
In the case of Knights Landing, the assembly in the listing below shows that the bitwise operations on the three operands are performed in 2 steps using 2 instructions: vpand and vpor. These instructions operate on XMM registers and belong to AVX instruction set.
vmovdqu (%rdi), %xmm0 #5.14 c1
vpand (%rsi), %xmm0, %xmm1 #5.21 c3
vpor (%rdx), %xmm1, %xmm2 #5.28 c5
vmovdqu %xmm2, (%rsi) #5.7 c7 Listing 79: Lines from assembly code for vector length support example on Knights Landing.
Optimization report for Knights Landing is shown in the listing below.
LOOP BEGIN at VL.c(4,3)
remark #15300: LOOP WAS VECTORIZED
remark #15450: unmasked unaligned unit stride loads: 3
remark #15451: unmasked unaligned unit stride stores: 1
remark #15475: --- begin vector cost summary ---
remark #15476: scalar cost: 13
remark #15477: vector cost: 1.000
remark #15478: estimated potential speedup: 7.420
remark #15488: --- end vector cost summary ---
LOOP ENDListing 80: Optimization report for vector length support example on Knights Landing.
4. Applicability of AVX-512
Intel Advanced Vector Extensions 512 (Intel AVX-512) is a major refresh of the vector instruction set for modern Intel architecture processors. The first processor families to support it are Intel Xeon Phi processor family x200 (formerly Knights Landing) and Intel Xeon processor Scalable family (formerly Skylake). AVX-512 consists of multiple modules (AVX-512F, -CD, -ER, -PF, -BW, -DQ, -VL, and several more modules expected in future processors), and different architectures support different sets of modules.
In our discussion of AVX-512, we saw that its innovations allow computational applications to take advantage of data parallelism better than with earlier instruction sets. Processors based on the Skylake architecture, compared to their predecessors based on the Broadwell architecture, have access to:
- wider vectors (512-bit up from 256-bit);
- more registers per core (32 registers up from 16);
- conflict detection instruction;
- bitmask-enabled vector arithmetics (as opposed to register-stored masks);
- instructions for vectorized data compress/expand, shuffle, and gather/scatter;
- functionality that frees up the register space and reduces the instruction count: embedded broadcasting and ternary logic; and
- embedded rounding for quick adjustment of the rounding mode for individual instructions.
Processors based on the Knights Landing architecture have a different subset of AVX-512 functionality. Compared to Skylake, they can vectorize
- high-precision exponential, reciprocal and reciprocal square root functions and
- prefetching of scattered memory addresses.
At the same time, in Skylake, compared to Knights Landing,
- there are additional 512-bit instructions for operations with double word (32-bit) and quadword (64-bit) integers and
- 512-bit instructions for arithmetics on byte-wide (8-bit) and word (16-bit) data types.
When you use automatic vectorization, you do not have to commit to a particular architecture. To switch the compilation target from Skylake to Knights Landing, you only need to change the compiler argument -xCORE-AVX512 to -xMIC-AVX512 (Intel compilers 18.x additionally require -qopt-zmm-usage=high for Skylake). You can also produce an executable that will work on both of these platforms by using -xCOMMON-AVX512, which restricts AVX-512 modules used in the executable to the ones that are common to Skylake and Knights Landing. However, one platform may be a better fit for your application than the other depending on the type of vector processing that you require and on a range of other factors.
Both Intel Xeon Scalable processors and Intel Xeon Phi processors are highly parallel and feature advanced vector processing capabilities. They differ in their balance between versatility and specialization, performance to cost ratio, and vector processing support. In the table below we compare the vector functionality in these processor families to help you make an informed decision regarding the best platform for your workloads.
| Function | SKL | KNL | Workload | Applications |
|---|---|---|---|---|
| AVX-512F: floating-point math |
Yes | Yes | Diverse | Engineering, physics, statistics, data analytics, energy applications |
| AVX-512F: fused multiply-add |
Yes | Yes | Dense linear algebra | Deep learning, engineering, fluid dynamics |
| AVX-512F: bitmasks |
Yes | Yes | Loops with branches | Classical machine learning, particle transport, software-defined visualization |
| AVX-512F: data compress/expand |
Yes | Yes | Sparse linear algebra | Mechanical engineering, seismic simulation, data analytics |
| AVX-512F: embedded rounding |
Yes | Yes | Discretization, numerical integration | Video transcoding, mathematical libraries |
| AVX-512F: gather/scatter |
Yes | Yes | Stencils, table lookups, sparse linear algebra | Weather modeling, plasma physics, data analytics |
| AVX-512CD: conflict detection |
Yes | Yes | Binning | Monte Carlo simulations: computational finance, physics; statistics and data analytics |
| AVX-512ER: transendentals |
Yes | N-body simulations, function approximation | Astrophysics, molecular dynamics, particle physics | |
| AVX-512PF: gather/scatter prefetch |
Yes | Stencils, table lookups, sparse linear algebra | Weather modeling, plasma physics, data analytics | |
| AVX-512DQ: large integers |
Yes | Encryption, random numbers | Security, statistics, Monte Carlo simulations, financial applications | |
| AVX-512BW: small integers |
Yes | Special data types | Game theory, signal processing, experimental data analysis, image manipulation | |
| AVX-512VL: shorter vectors |
Yes | Array-of-Structures data layouts | Legacy simulations of molecular dynamics, particle physics; classical machine learning |
Table 5: Comparison of vector functionality and application areas of Intel Xeon processor Scalable family (SKL) and Intel Xeon Phi processor family x200 (KNL).
The list of applications in the table above is only a rough guideline to the domains of applicability of the new AVX-512 vector instructions in Intel architecture. Furthermore, vectorization functionality is only one of the factors that you need to consider to identify the optimal architecture for a problem. The full scope of analysis for the choice of the best architecture includes:
- Memory architecture, including the size and speed of caches, access to high-bandwidth memory, non-uniform memory architecture versus symmetric multiprocessing.
- Multi-core organization, including the choice between high parallel scalability and resilience to under-subscription of the cores,
- Distributed-memory scalability options with modern high-performance network fabrics, and
- Cost and energy efficiency of the platform for a particular workload.
The choice of the computing platform for your task is a significant factor in application performance. However, the code that you run on your system may have far greater impact on your results. Numerous case studies of the recent years testify that code modernization may lead to performance improvements by orders of magnitude even on the same computing solution (see, e.g., 1, 2, 3 or 4).
To extract the best value out of your computing infrastructure investment, you need to assess how well the code base of your application takes advantage of modern processor features, including the multi-core architecture, vector instructions, hierarchical memory and high-performance networking. If the code uses legacy practices, it needs to be optimized before it can efficiently use Intel Xeon Scalable processors, Intel Xeon Phi processors, or any other modern processor family.
Colfax Research can help you to identify performance issues of your applications, optimize your code base, and help you to select the best platform for your needs. You can learn more about our consulting and contract research capabilities and engage with us at colfaxresearch.com.
Intel, Intel Xeon Phi and Xeon are trademarks of Intel Corporation or its subsidiaries in the U.S. and/or other countries.
*Other names and brands may be claimed as the property of others.