Optimization of Real-Time Object Detection on Intel® Xeon® Scalable Processors

This publication demonstrates the process of optimizing an object detection inference workload on an Intel® Xeon® Scalable processor using TensorFlow. This project pursues two objectives:
- Achieve object detection with real-time throughput (frame rate) and low latency
- Minimize the required computational resources
In this case study, a model described in the “You Only Look Once” (YOLO) project is used for object detection. The model consists of two components: a convolutional neural network and a post-processing pipeline. In this work, the original Darknet model is converted to a TensorFlow model. First, the convolutional neural network is optimized for inference. Then array programming with NumPy and TensorFlow is implemented for the post-processing pipeline. Finally, environment variables and other configuration parameters are tuned to maximize the computational performance. With these optimizations, real-time object detection is achieved while using a fraction of the available processing power of an Intel Xeon Scalable processor-based system.
![]() Colfax-Real-Time-Object-Detection.pdf (411 KB)
Colfax-Real-Time-Object-Detection.pdf (411 KB)
Demonstration:
Table of Contents
- 1. Real-time Object Detection
- 2. TensorFlow and MKL
- 3. Optimization of CNN
- 3.1. YOLO
- 3.2. Fusing layers
- 4. Optimization of Post-processing
- 4.1. Naive for-loops
- 4.2. NumPy Vectorization
- 4.3. TensorFlow
- 5. Tuning Parallelism
- 5.1. Selecting Cores
- 5.2. OpenMP Thread Count
- 5.3. Thread Affinity
- 5.4. OpenMP Block Time
- 5.5. Session Configurations
- 6. Benchmarks
- 6.1. System configuration
- 6.2. Batch Size
- 6.3. Optimization Results
- 6.4. Single-Frame Inference
- 6.5. Mini-Batch Inference
- 7. Conclusion
1. Real-time Object Detection
The advancement of convolutional neural networks (CNNs) and deep learning (DL) in the past decade brought about significant improvements in computer vision. One of the beneficiaries of these advances is the task of object detection, where the objective is to detect and locate real-world objects inside images or videos. This differs from basic image classification in that the machine learning model has to detect multiple objects in a single frame, and also determine where these objects are located. Figure 1 below shows an example of object detection. Recent research efforts, such as Faster R-CNN, Fastest DPM and YOLO (see also this blog post), have greatly improved both accuracy and speed of object detection. The advances in techniques, combined with the improved computer hardware, put real-time object detection well within the capabilities of modern processors.

Figure 1: Example of Object detction. Image is a frame out of the Caltech Pedestrian Dataset video (see Dollár et al. (2012)
Performing object detection in real time has a wide range of applications, from security surveillance to assistive technology, marketing, manufacturing and autonomous driving. For many of these applications, deployment would require high frame rate (number of frames processed per second), as well as low latency between image capture and object detection. Furthermore, they often benefit from minimizing the amount of resources used for running real-time analysis. For example, in Internet of Things (IoT) applications, which may be processing multiple inputs at once or working on other tasks concurrently with object detection, minimizing the amount of computational resources for object detection allows more resources to be allocated for other tasks. Therefore, this paper approach object detection with two goals:
- Achieve real-time frame rate and latency.
- Minimize required computational resources.
There is no universal definition of real-time frame rate. Instead, the definition of “real-time” is the “same rate as the input”, so the required frame rate will depend on the application. There are three reference point values used in this paper: 15 fps (common frame rate of CCTV cameras), 24 fps (typical frame rate of movies) and 30 fps (frame rate used for Caltech Pedestrian Dataset). The unit “fps” stands for “frames per second”.
Frame rate is a good metric for applications where the processing throughput is more important than the latency of processing a single frame. Offline processing of video streams is an example of such an application. In contrast, there exist applications that require object detection in a frame as fast as possible. For example, self-driving vehicles need to respond to the road conditions fast, and object detection speed in this application is best measured by latency.
Depending on whether an application needs a high frame rate or low latency, object detection can be approached differently. For latency minimization, one may choose to use all the available resources to process a single frame at a time, even if it leads to sub-optimal utilization of a powerful computing system. For throughput maximization, the mini-batch approach (processing several frames at once) may be better as it takes better advantage of a parallel computing system. Finally, if the latency is important, but mini-batch results in an acceptable latency, then this approach can minimize the utilization and free up the processing power for other tasks.
The aim of this work is to meet the required frame rate or latency while using the minimum amount of computing resources, and both the single-frame inference and the mini-batch approaches are studied.
This project is using the algorithm proposed in the YOLO project, which is described in Section 3. Original work on YOLO used the Darknet neural network framework, but for this work the network is implemented using TensorFlow.
The target platform for this paper is an Intel Xeon Scalable processor (formerly Skylake) from the Platinum group. These are highly parallel socket-mountable server processors with a large number of physical cores and support for AVX-512 vector instructions. The test system used in benchmarks contains 24 cores per socket, with total of 48 cores in a dual-socket system.
2. TensorFlow and MKL
Most machine learning workloads spend the vast majority of the execution time on floating-point arithmetic operations. So, in order to discuss floating-point performance, it is important to take note of the underlying mathematics engine. High-level machine learning frameworks often use external linear algebra libraries, such as OpenBLAS, to drive their math engines. TensorFlow natively uses the Eigen library for its operations, but recently there has been a joint effort made by the TensorFlow team and Intel Corporation to add support for Intel Math Kernel Library (MKL). Intel MKL is a highly optimized mathematics library with support for operations in linear algebra, such as matrix product, and neural network operations, such as convolution. The use of MKL can significantly increase the speed of TensorFlow on Intel architectures. Therefore, this project uses TensorFlow with the Intel MKL back-end.
Some of the tuning methods discussed in Section 5 are specific to MKL and therefore can be applied to other deep learning frameworks that are capable of using this library, such as Caffe, Neon, Theano or Torch.
3. Optimization of CNN
This work focuses on deep learning inference using a pre-trained model, so additional speedup can be achieved by removing or combining layers that are not necessary for inference. This section first describes the YOLO network, and then describes the changes that were made on the network in order to increase its speed.
3.1. YOLO
“You Only Look Once” (YOLO) is a convolutional neural network designed for fast object detection. Compared to other similar models, YOLO’s strength is that it frames object detection as a regression problem for bounding boxes with a single-pass pipeline. Others models typically have two passes through one or more pipelines: region proposal and then classification. This single pass is one of the attributes that makes it extremely fast.
In the original git repository there are multiple YOLO models with a range of depths. The deeper networks typically give a better detection precision but take longer. The implementation presented in this paper uses the shallower 9-layer network, “Tiny YOLO” (see Table 1). Each of the 9 layers in “Tiny YOLO” are convolution layers; there are no fully-connected layers. All but the last convolution is followed by a Leaky ReLU activation and batch normalization.
The original model has been trained on the Pascal VOC dataset with 20 object categories, and it achieves 52.6 Mean Average Precision (mAP). To run the TensorFlow implementation of the CNN, the original Darknet model was converted the TensorFlow format.
| Input (416x416x3) |
|---|
| Conv3-16 s-1 |
| MaxPool2 s-2 |
| Conv3-32 s-1 |
| MaxPool2 s-2 |
| Conv3-64 s-1 |
| MaxPool2 s-2 |
| Conv3-128 s-1 |
| MaxPool2 s-2 |
| Conv3-256 s-1 |
| MaxPool2 s-2 |
| Conv3-512 s-1 |
| MaxPool2 s-1 |
| Conv3-1024 s-1 |
| Conv3-1024 s-1 |
| Conv1-125 s-1 |
| Output (13x13x125) |
Table 1: Tiny YOLO CNN layers
3.2. Fusing layers
For inference workloads, it is possible to fuse the batch normalization and convolution layers, which may improve the frame rate and latency. After fusing, the new weights and biases for each layer can be obtained by the expressions (1) and (2).
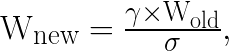 (1)
(1)
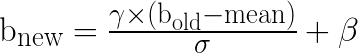 (2)
(2)
Here, W is the weight and b is the bias. β, γ, σ and mean are parameters of batch normalization. Each of the first 8 convolution layers of Tiny YOLO has batch normalization. In this work, the matching batch normalization and convolution layer parameters are fused into new weight and bias parameters for the convolution layer.
4. Optimization of Post-processing
The output array of the CNN pipeline is directed into the next step of the YOLO algorithm, the processing pipeline. There, the CNN output is processed and converted into a form that can be fed to the non-max suppression (NMS) kernel. This section demonstrates how to implement the processing pipeline in a pure vectorized format, instead of relying on for-loops. Note that all reference to vectorization in this paper is in the context of array programming, not SIMD parallelism.
4.1. Naive for-loops
“Naive for-loops” implementation uses a mix of Python for-loops and NumPy operations. The CNN part of YOLO (see Table 1) outputs a 13×13 feature map with depth of 125 (13x13x125), the corresponding to 5 bounding boxes, and class predictions for each location on the map (13x13x5 predictions). Each bounding box prediction consists of 25 values: the first 4 values are {x,y,w,h} of the box, the 5th value is the confidence that the box contains an object, and the last 20 values are the 20 class probabilities. The detection score for each box is the product of the confidence value and the maximum class probability. This score is checked against a user-defined threshold value to filter out low-confidence results.
The final outputs of this section are three arrays: boxes that pass the threshold, scores of these boxes, and classes associated with these boxes. The output arrays will be processed through NMS, which eliminates the overlapping boxes by suppressing the boxes that have inferior scores.
The difficulty of implementing this code section is the fact that the array is heterogeneous in that the 25 consecutive values for a box contain different types of data that require different processing. Listing 1 shows the naive for-loop implementation. The main body of this function consists of the 3 nested for-loops going through each pixel and bounding boxes. For-loops add a significant overhead to this particular implementation, drastically reducing the speed.
anchors= # array of anchor boxes
boxes=[]
scores=[]
classes=[]
# over all the pixels and boxes
for cy in xrange(13):
for cx in xrange(13):
for b in xrange(5):
off=b*25
#get confidence value
tc=preds[cy][cx][off + 4]
conf=sigmoid(tc)
pos=off+5
#get class prediction and max
# class probability
class_p=preds[cy][cx][pos:pos+20]
class_p=softmax(class_p)
max_idx=np.argmax(class_p)
max_score=classes[class_idx]*conf
#confidence threshold
if(max_score > 0.20):
scores +=[max_score]
classes+=[max_idx]
#extract box location
tx=preds[cy][cx][off + 0]
ty=preds[cy][cx][off + 1]
tw=preds[cy][cx][off + 2]
th=preds[cy][cx][off + 3]
x=(float(cx) + sigmoid(tx))*32.0
y=(float(cy) + sigmoid(ty))*32.0
w=anchors[2*b ]*np.exp(tw)*16.0
h=anchors[2*b+1]*np.exp(th)*16.0
x1=x-w
x2=x+w
y1=y-h
y2=y+h
boxes+=[[x1,y1,x2,y2]]Listing 1: Naive for-loop implementation
4.2. NumPy Vectorization
The NumPy library contains many useful array operations that allow a pure vectorized implementation as shown in Listing 2.
boxes=[]
scores=[]
classes=[]
preds=preds.reshape(13,13,5,25)
# slice confidence and predictions
conf=sigmoid(preds[:,:,:,4])
class_p=softmax(preds[:,:,:,5:25])
max_idx=np.argmax(class_p,axis=3)
max_score=np.amax(class_p,axis=3)*conf
# check against threshold
ind=np.where(max_score>0.20)
scores =max_score[ind]
classes=max_idx[ind]
#slice selected box cordinates
tx=(preds[:,:,:,0])[ind]
ty=(preds[:,:,:,1])[ind]
tw=(preds[:,:,:,2])[ind]
th=(preds[:,:,:,3])[ind]
x=(ind[1] + sigmoid(tx))*32.0
y=(ind[0] + sigmoid(ty))*32.0
w=anchors[2*ind[2] ]*np.exp(tw)*16.0
h=anchors[2*ind[2]+1]*np.exp(th)*16.0
x1=x-w
x2=x+w
y1=y-h
y2=y+h
boxes=np.array([x1,y1,x2,y2]).T.copy()Listing 2: NumPy vectorization
The original input 13x13x125 array can be reshaped to 13x13x5x25 to isolate individual bounding box predictions. This new shape allows for easier NumPy array slicing to separate the coordinates, confidence scores, and the class probabilities. Using NumPy array operations and broadcasting, the confidence scores and the maximum class probabilities can be computed and multiplied, resulting in an array form of max_score.
The naive implementation has an if-statement at this point, comparing each max_score to the threshold. In order to apply a conditional to an array, the NumPy implementation uses the logical operator and the numpy.where() function. The > operator applied to a NumPy array is broadcast, and it returns a boolean array. The numpy.where() function, given a single boolean array input, will return the indices of the True elements. These indices can then be used to get the corresponding box coordinates, confidence values and class predictions.
4.3. TensorFlow
Finally, we convert the NumPy implementation to TensorFlow API as shown Listing 3.
preds=tf.reshape(preds,[13,13,5,25])
# slice confidence and predictions
confs=tf.sigmoid(preds[:,:,:,4])
class_p=tf.nn.softmax(
preds[:,:,:,5:25])
max_score=tf.reduce_max(
class_p,axis=3)*confs
max_idx=tf.argmax(class_p,axis=3)
# check against threshold
ind=tf.where(max_score>0.20)
scores =tf.gather_nd(max_score,ind)
classes=tf.gather_nd(max_idx,ind)
#slice selected box cordinates
tx=tf.gather_nd(preds[:,:,:,0],ind)
ty=tf.gather_nd(preds[:,:,:,1],ind)
tw=tf.gather_nd(preds[:,:,:,2],ind)
th=tf.gather_nd(preds[:,:,:,3],ind)
ind=tf.transpose(ind)
x=(tf.cast(ind[1],tf.float32) +
tf.sigmoid(tx))*32.0
y=(tf.cast(ind[0],tf.float32) +
tf.sigmoid(ty))*32.0
w=tf.gather(anchors,2*ind[2])*
tf.exp(tw)*16.0
h=tf.gather(anchors,2*ind[2]+1)*
tf.exp(th)*16.0
x1=x-w
x2=x+w
y1=y-h
y2=y+h
boxes=tf.stack([x1,y1,x2,y2],axis=1)Listing 3: TensorFlow implementation
While both the NumPy and TensorFlow implementations are vectorized, the latter has an advantage. The output of the data processing section is fed into NMS. Because we have committed to using TensorFlow, it makes sense to call a built-in TensorFlow method for NMS, tf.image.non_max_suppression(). Therefore, there are two transitions between frameworks: from TensorFlow to NumPy after CNN and from NumPy to TensorFlow for NMS. The transitions between frameworks combined with the extra session.run() for NMS add a significant overhead for some versions of TensorFlow.
To avoid this overhead, the final implementation uses TensorFlow array programming.
Fortunately, the TensorFlow API for slicing is nearly identical to the NumPy API, and it has equivalents to NumPy methods like tf.where(), tf.gather() and tf.gather_nd(), which are necessary for our application.
5. Tuning Parallelism
After the code optimization steps described above, the inference engine calls TensorFlow methods for most of the calculations. Even though TensorFlow with the Intel MKL back-end uses highly-optimized code base for calculations, some arguments of the parallel algorithms can be tuned to extract more power from the Intel CPU-based computing platform. There are three points of access to these tuning parameters: system environment variables, tf.Session() configuration arguments, and Linux commands, as described in this section. The recommended settings of these parameters come from the CPU optimization page of the TensorFlow website.
In this context, we will talk about OpenMP, which is a parallel programming API supported in most modern C, C++ and Fortran compilers. The Intel implementation of OpenMP is used for multi-threading inside the MKL back-end.
5.1. Selecting Cores
The goal of this work is to use as little resources as possible to achieve the desired frame rate, so that the rest of the system can be used by other tasks. To partition the resources (processor cores) between object detection and other processes, our implementation uses taskset. This Linux utility allows users to restrict a process to a list of logical processors.
The strategy for choosing the list of logical processors for object detection is dictated by three factors: the desired number of physical cores, hyper-threading, and NUMA locality. The approach of this work is this:
- The number of physical cores for object detection is determined by the user. The tests of the frame rate discussed in Section 6 vary this number from 1 to 48 because the target system contains 48 physical cores.
- With the core count fixed, we select two logical processors on each core. This is done to take advantage of the Intel Hyper-Threading technology, which allows each core of Intel Xeon Scalable processors to operate as two logical CPUs. Using both hyper-threads improves the calculation speed in applications with complex memory traffic.
- If the number of physical cores is less than the number of cores per socket (in our case, 24), then all selected cores should be on the same NUMA node. This improves the calculation speed by ensuring that data traffic never has to go across the interconnect between the CPU sockets. On the target system, a NUMA node consists of all cores within the same CPU socket (this is applicable to Intel Xeon Scalable processors with cluster-on-die functionality disabled).
The arguments of taskset must refer to logical processors by their OS procs (numerical identifiers). The mapping of OS procs to cores can be found in /proc/cpuinfo. The list of OS procs belonging to a NUMA node, as well as the list of NUMA nodes can be found by running the command numactl -H.
user@host% # Using 16 OS procs, but only 8 cores
user@host% taskset -c 0-7,48-55 ./inference.pyHere OS procs 0 through 7 are all on different cores, but on the same socket. OS proc 48 shares the physical core with 0, 49 shares with 1, 50 shares with 2, etc.
Section 5.3 discusses the environment variable KMP_AFFINITY used for pinning software threads to OS procs. This configuration parameter is complementary to taskset because taskset controls the affinity of all threading frameworks, while KMP_AFFINITY only controls the Intel OpenMP library.
5.2. OpenMP Thread Count
Restricting the resources with taskset does not, in itself, tell the application how many software threads to use. However, many architecture-aware libraries will use as many threads as the number of logical processes made available by taskset. This means, for our configuration, two software threads per physical core. While it makes sense for the stages of the calculation that benefit from hyper-threading, it does not work well for MKL functions, where memory traffic is well-controlled in code. For example, the MKL implementation of SGEMM used in CNN inference prefers 1 thread per core. For this reason, the recommended optimization for TensorFlow is to set the environment variable OMP_NUM_THREADS equal to the number of physical cores.
For example, to use 8 physical cores in the scope of this work, with 8 threads used in MKL, but 16 logical processors available to other parallel parts of the calculation, we use the following:
user@host% # Tell OpenMP to use 8 threads
user@host% export OMP_NUM_THREADS=8
user@host% # Using 16 OS procs, but only 8 cores
user@host% taskset -c 0-7,48-55 ./inference.py5.3. Thread Affinity
The KMP_AFFINITY variable controls the core affinity of the OpenMP runtime, allowing users to control the pinning of OpenMP threads to the physical cores. For example, KMP_AFFINITY=compact can be used to put neighboring threads on neighboring cores, allowing for better cache sharing. Conversely, KMP_AFFINITY=scatter can be used to map the OpenMP threads physically far apart from each other. The recommended setting for KMP_AFFINITY on TensorFlow is:
export KMP_AFFINITY=granularity=fine,compact,1,0The first part, granularity=fine, forbids thread migration. By default, the Linux operating system is allowed to transfer a software thread from one physical core to another. This often causes heavy cache misses because the new core has a different L2 or L1 cache from the original. Preventing the migration will prevent these unnecessary cache misses.
The second part, compact,1,0, controls the mapping of the threads to cores. The compact argument places OpenMP threads physically as close to each other as possible. However, this can have drawbacks in systems with enabled Intel Hyper-Threading technology, where multiple thread contexts can reside on the same core. With hyper-threading and compact, consecutive threads will be assigned to the same physical core. With hyper-threading and compact,1, consecutive threads will be assigned to different physical cores on the same CPU socket. The ,0 part of the variable is the offset, which determines the starting number for the core mapping. An offset of zero is default, and a greater offset is useful for running multiple processes in such a way that they don’t contend for cores.
5.4. OpenMP Block Time
The KMP_BLOCKTIME variable controls the wait time in milliseconds after the end of a parallel region that an OpenMP thread should wait before going to sleep. A large value of KMP_BLOCKTIME would mean that the OpenMP threads are kept “hot” for a long time, and when a new parallel region starts, its setup will require a smaller overhead compared to if it was sleeping. By default, KMP_BLOCKTIME is set to 200 milliseconds. Although a large KMP_BLOCKTIME is favorable for pure OpenMP applications, it can be detrimental if the application has other parallel frameworks because a large block time of can starve these other frameworks of the necessary compute resources.
KMP_BLOCKTIME for TensorFlow is a tuning parameter, and the optimal value depends on the model and dataset that is being used. The recommended range for TensorFlow is between 0 to 30 milliseconds. In the case of YOLO, the optimal value is empirically found to be 1 millisecond.
5.5. Session Configurations
TensorFlow Session object has multiple configuration parameters that can affect the behavior of its execution.
The two parameters that are used for parallelism tuning are:
- inter_op_parallelism_threads
- intra_op_parallelism_threads
Both parameters control threading behavior of operations. These parameters can be set as follows:
xconfig=tf.ConfigProto(
inter_op_parallelism_threads=1,
intra_op_parallelism_threads=8);
tf.Session(config=config)The inter_op_parallelism_threads parameter controls how many independent operations can run simultaneously. For example, during back-propagation of neural networks, the gradients for the weights of a layer can be computed independently of the gradients for the bias. If inter_op_parallelism_threads is greater than 1, TensorFlow may execute these two operations simultaneously. However, operations with dependencies cannot run simultaneously: layer 2 of a network can not run simultaneously with layer 1. The recommendation for TensorFlow is to set inter_op_parallelism_threads equal to the number of NUMA nodes available. For Intel architecture processors, this is usually equal to the number of the CPU sockets (or a multiple thereof if the sub-NUMA clustering or cluster-on-die functionality is enabled). The total number of NUMA nodes can be found with numactl -H
For the YOLO inference workload, the optimal setting of inter_op_parallelism_threads is 1. This agrees with the recommended value: although the system has 2 NUMA nodes, taskset is used to restrict execution to the cores inside the same NUMA node.
The intra_op_parallelism_threads parameter controls the number of threads that a single operation can use. This has the same functionality as OMP_NUM_THREADS, but affects operations that do not rely on OpenMP for threading. The recommendation for TensorFlow is to set intra_op_parallelism_threads equal to OMP_NUM_THREADS.
6. Benchmarks
6.1. System configuration
The frame rate measurements presented in this section are conducted on a Colfax CX1260i-T-X7 server based on a dual-socket Intel® Xeon® Platinum 8160T processor with 192 GB of DDR4 memory at 2400 MHz. The processor has 24 cores per socket with 2-way hypert-hreading, so this system has 48 physical cores presenting themselves as 96 logical processors. The operating system used is CentOS 7.4. Python 2.7 from the Intel Distribution for Python 2018 is used with TensorFlow version 1.4.0 and OpenCV version 3.3.1-dev.
The computation rate is reported as throughput in units of frames per second (fps).
6.2. Batch Size
For single-frame inference, the effective frame rate is related to the processing time (latency) according to Equation 3.
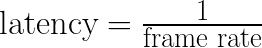 (3)
(3)
For mini-batch inference (object detection in several frames concurrently), the frame rate is computed from the time (latency) it takes to process the mini-batch as shown in Equation 4.
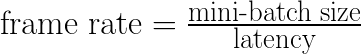 (4)
(4)
Single-frame inference is the usage scenario when object detection in a given frame must be performed as fast as possible — for example, in a self-driving vehicle. Mini-batch inference may allow the user to process more frames per second than single-frame inference, but the application must wait for the entire batch to finish processing before any result can be used. This approach will generally have worse latency, but better frame rate than single-frame processing. The mini-batch approach is useful in offline data processing, when the latency less important than throughput. It can also help to achieve a target latency with fewer cores. Mini-batch size of 1 is equivalent to single-frame processing.
6.3. Optimization Results
Figure 2 shows the frame rate gains due to the optimizations presented in this paper for single-frame processing (i.e., a mini-batch size of 1).
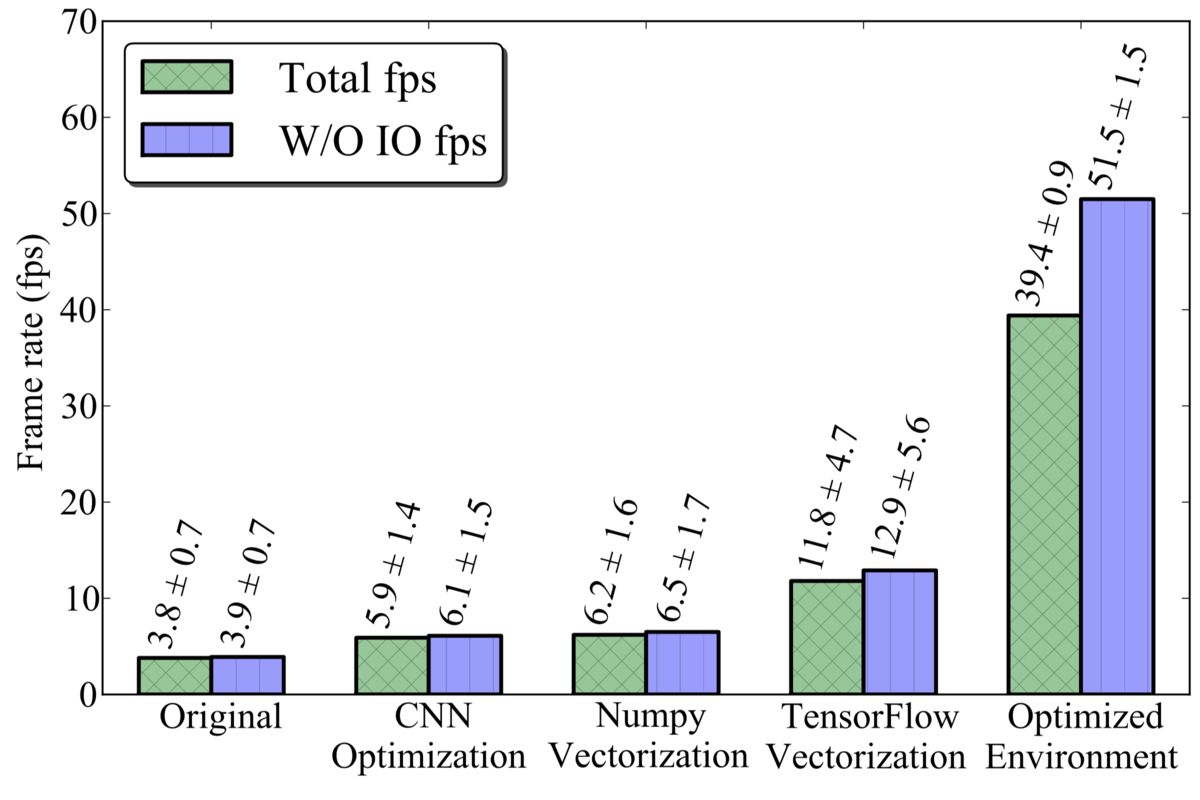
Figure 2: Impact of code optimization.
Each measurement is done over processing of 500 frames, with time for each frame measured independently. The times for the first 100 frames (≈3 seconds) are ignored in order to avoid fluctuation from issues like initialization and leaving CPU power saving states. The average times and the standard deviation is reported from the latter 400 frame times. For these benchmarks, the number of threads is kept constant at 8 threads, or one-sixth of the total computational capacity.
Two values for frame rate are reported: total frame rate and frame rate without I/O. Total frame rate includes the time taken to load the frames and display them in OpenCV, so this number is dependent on the some external factors like the properties of the video capturing device. For the benchmark setup, the I/O took up to 20% of the total wall-time. The frame rate without I/O is reported to give the best-case speed of the application.
In Figure 2, Original represents a naive model consisting of CNN with batch normalization and postprocessing from Listing 1. CNN optimization is the network optimization presented in Section 3. Optimizations for the NumPy Vectorization and TensorFlow Vectorization cases are discussed in Section 4. Finally, Optimized Environment is discussed in Section 5. All optimizations combined deliver 10x improvement for the total frame rate and around 13x for frame rate without I/O.
6.4. Single-Frame Inference
The optimizations discussed above were also applied to YOLO-V2 CNN. Figures 3 and 4 below show the total frame rate with respect to number of cores for “stressed” and “idle” systems for both Tiny-YOLO and YOLO-V2 CNN models.
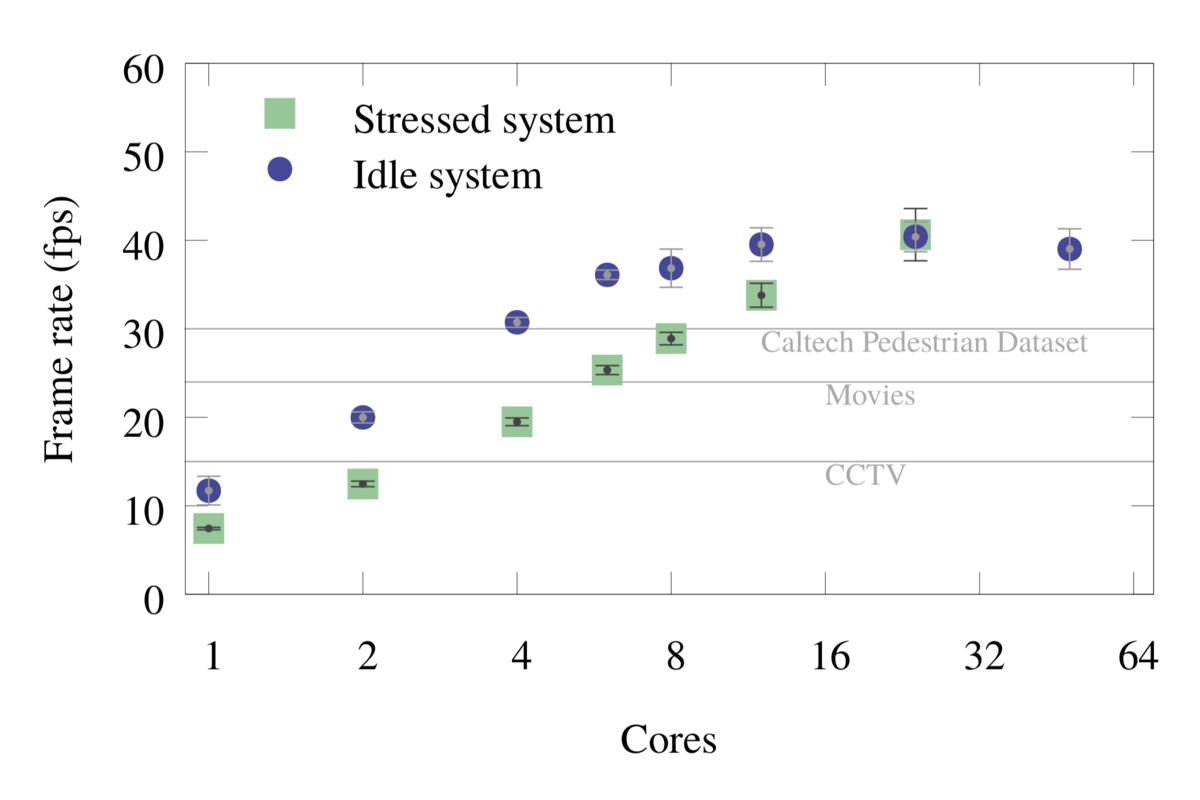
Figure 3: Tiny-YOLO: Single-frame inference timing, including I/O.
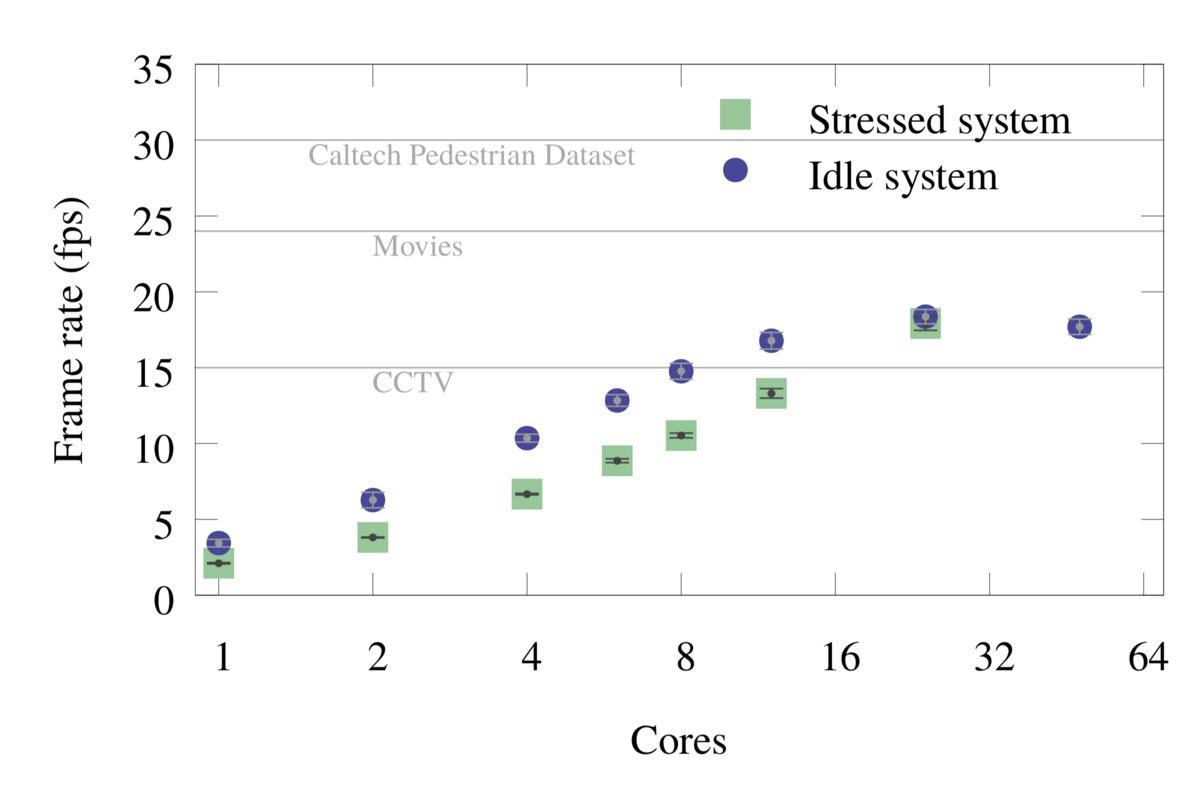
Figure 4: YOLO-V2: Single-frame inference timing, including I/O.
The same data is shown in tabulated format in Table 2 and 3.
| Cores | Stressed | Idle | ||
|---|---|---|---|---|
| Total | W/out IO | Total | W/out IO | |
| 1 | 7.4±0.1 | 7.9±0.1 | 11.7±1.6 | 12.7±1.8 |
| 2 | 12.4±0.3 | 13.9±0.4 | 20.0±0.6 | 22.6±0.7 |
| 4 | 19.5±0.4 | 23.2±0.6 | 30.7±0.6 | 37.6±0.7 |
| 6 | 25.3±0.5 | 31.4±0.7 | 36.1±0.5 | 46.0±0.8 |
| 8 | 28.9±0.7 | 36.8±1.1 | 36.9±2.2 | 47.6±3.5 |
| 12 | 33.7±1.3 | 45.1±2.3 | 39.5±1.9 | 52.7±3.1 |
| 24 | 40.6±3.0 | 57.7±5.8 | 40.4±1.7 | 56.1±2.5 |
| 48 | 39.0±2.3 | 53.3±4.2 | ||
Table 2: Tiny-YOLO: Single-frame inference timing. The values are in frames per second (fps).
| Cores | Stressed | Idle | ||
|---|---|---|---|---|
| Total | W/out IO | Total | W/out IO | |
| 1 | 2.1±0.04 | 2.1±0.04 | 3.4±0.2 | 3.5±0.2 |
| 2 | 3.8±0.03 | 3.9±0.03 | 6.2±0.5 | 6.4±0.5 |
| 4 | 6.6±0.05 | 6.9±0.05 | 10.3±0.2 | 10.8±0.3 |
| 6 | 8.8±0.12 | 9.2±0.13 | 12.8±0.4 | 13.6±0.4 |
| 8 | 10.5±0.15 | 11.1±0.16 | 14.7±0.5 | 15.7±0.5 |
| 12 | 13.3±0.31 | 14.2±0.32 | 16.7±0.5 | 18.0±0.6 |
| 24 | 17.9±0.44 | 19.5±0.48 | 18.3±0.4 | 19.9±0.5 |
| 48 | 17.6±0.5 | 19.6±0.4 | ||
Table 3: YOLO-V2: Summary of frame rate measurements in fps.The values are in frames per second (fps).
In the “idle” run, the object detection application is the only computationally heavy application running on the system. In the “stressed” run, the object detection application is run on a subset of the cores, and the rest of the cores are used for a large matrix product calculation (Intel MKL SGEMM). This test simulates multi-tenancy, where a server is running many applications concurrently. There is a large difference between the two scenarios for low core count benchmarks, largely due to the Intel Turbo Boost feature of the processor. When the CPU utilization is low, as in the case of low core count “idle” runs, the processor is allowed to increase its frequency up to the maximum Turbo frequency as long as the power consumption on the CPU is below the threshold value (TDP). For the CPU used in this benchmark, the frequency can scale from the maximum Turbo frequency of 3.0 GHz to the base frequency of 2.1 GHz. For more on Turbo Boost in Intel Xeon Scalable processors, see this paper. In contrast, for the “stressed” runs, the CPU is fully occupied even when few cores are used for object detection, so it does not benefit as much from the Turbo Boost. The difference between the “idle” and the “stressed” speed reduces as the core count is increased, and it goes away when one CPU is fully utilized (24 cores). Note that the Turbo frequency is set based on the core occupancy of a socket, so the difference goes away at 24, rather than 48, cores because it does not matter if the second socket is utilized or not.
For Tiny-YOLO model, each core constitutes 2.1% of the total computational resource of the test system. For the idle system, the low CCTV frame rate of 15 fps can be achieved with just 2 cores, and both the typical movie frame rate of 24 fps and the Caltech Pedestrian Dataset frame rate of 30 fps at 4 cores. For the fully stressed system, the required resources are 2 cores to achieve CCTV frame rate, 6 cores for a typical movie frame rate, and 8 to 12 cores for the Caltech Pedestrian Dataset frame rate. These serve as maximum and minimum cases for the system utilization outside the detection workload. So in real-case scenarios, where the object detection is running concurrently with other workloads, the required core count will fall somewhere in between the values. The speed without I/O that we quote can potentially be achieved, for example, if the I/O is done on a separate thread. In this case, the 30 fps mark is achieved with 4-6 threads.
YOLO-V2 model has 23 convolution layers compared to 9 convolution layers in Tiny-YOLO. It has an increased object detection precision at the cost of speed, which is quite evident in the frame rate plots. The YOLO-V2 model requires at least 12 cores to reach the CCTV frame rate of 15 fps.
Finally, there are two important notes about this result.
- MKL integration into TensorFlow is in its early stages, an Intel MKL is continually upgraded. Although this is already an impressive showing, the floating-point operation rate of the “Tiny YOLO” model for single-frame inference is still short of the theoretical peak floating-point operation rate of the test system. According to the authors of YOLO, “Tiny YOLO” inferencing requires 6.97ċ109 floating-point operations. Using our measured frame rate, this number can be translated to floating-point operation rate in GFLOP/s (billions of floating-point operations per second). The single precision theoretical peak of the test system in the “idle” scenario is 1.54 TFLOP/s with 8 cores and 3.07 GFLOP/s with 24 cores. The timing of of “Tiny YOLO” translates to 331 GFLOP/s with 8 cores or 391 GFLOP/s with 24 cores. This amounts to an efficiency of 22% and 13%, respectively. As Intel MKL and TensorFlow improve, the required computational resource may decrease even further.
- The low efficiency and poor frame rate scaling with core count is due to the self-imposed limitation of single-frame reference (i.e., batch size of 1) in these tests. Modern processors are highly parallel, and there aren’t enough independent parallelizable elements in the workload with a batch size of 1. At larger batch sizes, the object detection frame rate scales better with the number of cores. Mini-batch inference timing is described in Section 6.5.
6.5. Mini-Batch Inference
In this section, the timing results for mini-batch inference are presented. In all test cases, 24 cores (i.e., one complete socket) of the processor are used.
Figures 5 and 6 show the frame rate and latency plots for mini-batch inference for both Tiny-YOLO and YOLO-V2. The horizontal markings in the latency plots are of special importance because they show the required minimum latencies of Caltech pedestrian dataset, Movies and CCTV for mini-batch size of 1.
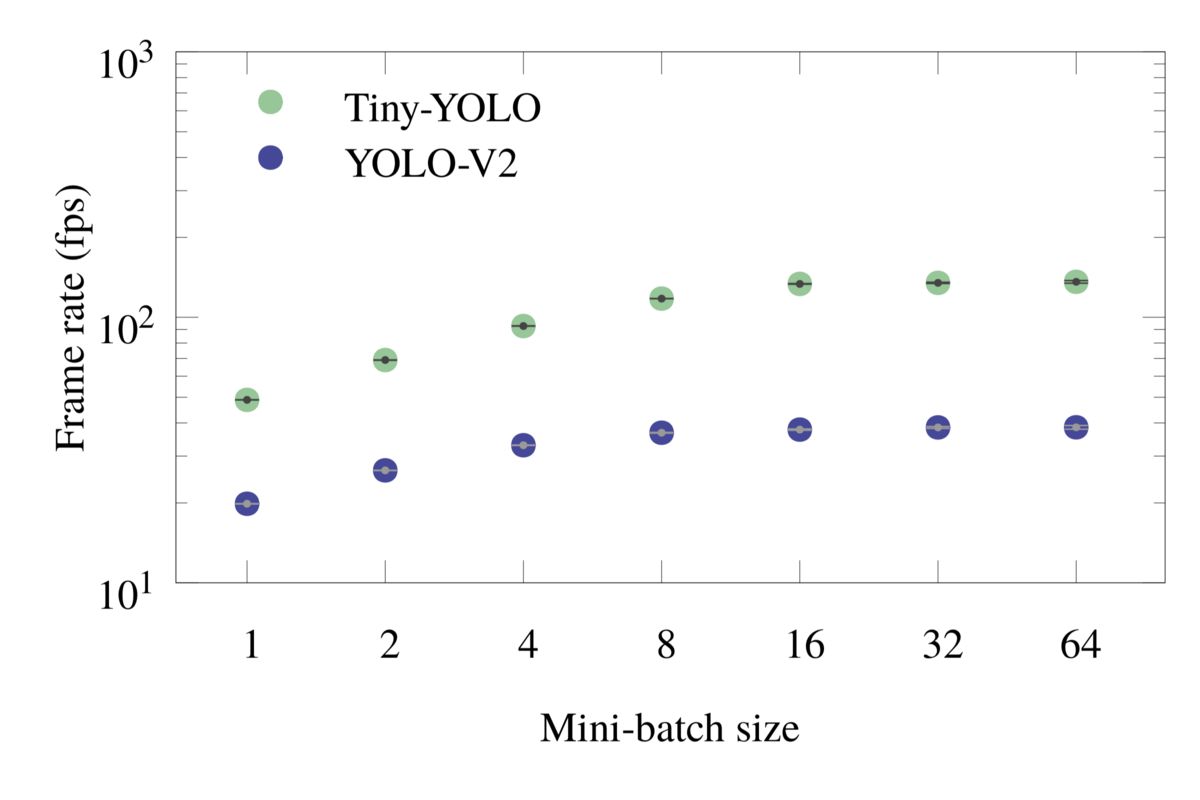
Figure 5: Frame rate for mini-batch object detection with 24 cores, without I/O.
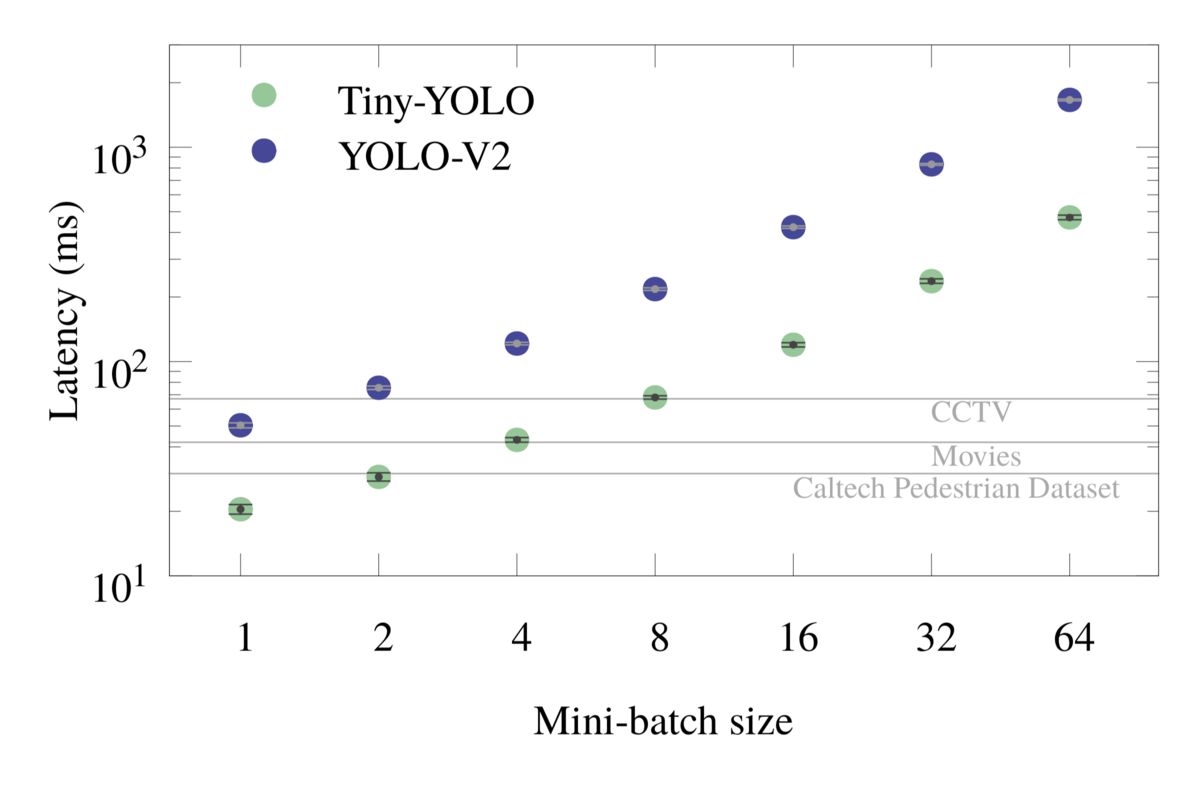
Figure 6: Latency for mini-batch object detection with 24 cores, without I/O.
The data used for these plots is summarized in Tables 4 and 5.
| Batch size | Latency (ms) | |
|---|---|---|
| Tiny-YOLO | YOLO-V2 | |
| 1 | 48.8±0.1 | 19.8±0.0 |
| 2 | 69.0±0.1 | 26.5±0.0 |
| 4 | 92.7±0.1 | 32.9±0.1 |
| 8 | 117.6±0.1 | 36.7±0.1 |
| 16 | 133.6±0.4 | 37.7±0.2 |
| 32 | 134.8±0.7 | 38.5±0.3 |
| 64 | 136.0±1.6 | 38.5±0.6 |
Table 4: Batch inference frame rate with 24 cores.
| Batch size | Latency (ms) | |
|---|---|---|
| Tiny-YOLO | YOLO-V2 | |
| 1 | 20.4±1.0 | 50.4±1.3 |
| 2 | 28.9±1.3 | 75.4±1.3 |
| 4 | 43.1±1.0 | 121.3±1.7 |
| 8 | 68.0±1.2 | 217.7±3.0 |
| 16 | 119.7±2.8 | 423.5±5.4 |
| 32 | 237.2±5.7 | 831.6±7.9 |
| 64 | 470.5±11.6 | 1661.7±16.0 |
Table 5: Batch inference latency with 24 cores.
Processing several frames at once in a mini-batch utilizes the resources more efficiently. For instance, with 24 cores, Tiny-YOLO with a batch size of 8 delivers 836 GFLOP/s (27% efficiency) and with a batch size of 64 it operates at 949 GFLOP/s (31% efficiency). The heavier model YOLO-V2 with a batch size of 64 delivers 1350 GFLOP/s, which is 44% efficiency.
As a consequence, mini-batch inference with a large batch size should be the default strategy for offline image processing, when the latency is not important.
At the same time, if the latency is important, mini-batch processing may still be useful due to its improved efficiency. For example, using 24 cores and the Tiny-YOLO model, single-frame processing yields 40.6 fps, which is barely enough to concurrently support three CCTV cameras (15 fps each). With the same number of cores and the same model, mini-batch processing with a batch size of 8 has an effective frame rate of 118 fps, which is nearly enough to support eight CCTV cameras, still in real time (because the mini-batch is processed in 1/15th of a second),
7. Conclusion
This publication presents the optimization path for real-time object detection inference (based on the YOLO model) with TensorFlow. Observations of this work are characteristic of modern applications for highly-parallel processors. That is, the speed of the application and the efficiency of resource utilization depend critically on the design of the code and on the parallel strategy.
First, the paper demonstrated common techniques that improve computational efficiency in deep learning and data processing applications. They included:
- Algorithm optimizations that improve the data locality (in this paper, it was layer fusion in a CNN);
- Code transformation toward high-level APIs with architecture-aware back-end libraries (in this case, NumPy and TensorFlow with Intel MKL back-end);
- Resource partitioning and parallel algorithm control with environment variables and Linux tools.
The techniques mentioned above do not change the nature of the calculation, but, rather, make the application execute closer to the underlying hardware. Cumulatively, the difference in the calculation speed between a correct but inefficient code and the final optimized version was observed to be 13x.
Secondly, the measurements presented here show that the tradeoff between the computation speed and detection precision can be a tuning parameter of an artificial intelligence system. Substituting the Tiny-YOLO model for YOLO-V2 increases the frame rate by 2-3x at the cost of less accurate object detection.
Thirdly, the paper demonstrated that the choice of the parallel strategy on Intel architecture is a significant factor in the bottom-line efficiency:
- In a scenario where a single video feed is processed in real-time (e.g., a self-driving vehicle), the user can choose just enough CPU cores to handle object detection at the required frame rate. For instance, our benchmark system needs to dedicate 8-12 cores to detect objects in a 30 frames per second video feed, while the rest of the cores can be assigned to other tasks.
- In a scenario where multiple video feeds are processed (e.g., surveillance footage from multiple cameras), the user can choose to process object detection on a mini-batch of frames coming from the different feeds, rather on than a single frame. This would increase the amount of data the system can handle. In setup, the single-frame strategy allows each 24-core socket to process 3 (three) CCTV feeds, while the mini-batch strategy increases the capacity to 8 (eight) CCTV feeds, still maintaining real-time latency of 1/15th of a second.
The methods discussed in the paper are applicable to a broad range of data analysis and machine learning tasks targeting modern Intel architecture processors.