Intel® Python* on 2nd Generation Intel® Xeon Phi™ Processors: Out-of-the-Box Performance
This paper reports on the value and performance for computational applications of the Intel® distribution for Python* 2017 Beta on 2nd generation Intel® Xeon Phi™ processors (formerly codenamed Knights Landing). Benchmarks of LU decomposition, Cholesky decomposition, singular value decomposition and double precision general matrix-matrix multiplication routines in the SciPy and NumPy libraries are presented, and tuning methodology for use with high-bandwidth memory (HBM) is laid out.
Download as PDF: ![]() Colfax-Intel-Python.pdf (1 MB) or read online below.
Colfax-Intel-Python.pdf (1 MB) or read online below.
Code: coming soon, check back later.
See also: colfaxresearch.com/get-ready-for-intel-knights-landing-3-papers/

1. A Case for Python in Computing
Python is a popular scripting language in computational applications. Empowered with the fundamental tools for scientific computing, NumPy and SciPy libraries, Python applications can express in brief and convenient form basic linear algebra subroutines (BLAS) and linear algebra package (LAPACK) functions for operations on matrices and systems of linear algebraic equations.
The recently released 2nd generation Intel Xeon Phi processors (formerly codenamed Knights Landing, or KNL) have high performance capabilities in BLAS and LAPACK, which makes them well-suited as computing platforms for Python/NumPy/SciPy applications. However, the standard Python distribution, CPython, is not yet able to take advantage of the many integrated core (MIC) architecture that Intel Xeon Phi processors are based on.
To address this problem, Intel Distribution for Python uses the performance library Intel MKL to accelerate linear algebra. Additionally, this distribution provides interfaces to Intel Threading Building Blocks (TBB), Intel Data Analytics Acceleration Library (DAAL) and Intel Message Passing Interface (MPI) libraries.
In this publication we report on the usability and performance on Intel Xeon Phi processors of an essential subset of BLAS and LAPACK: LU decomposition, Cholesky decomposition, singular value decomposition (SVD) and general matrix-matrix multiplication. We compare the benchmarks taken with CPython to those taken with Intel Python.
2. Benchmarks
The core of the benchmark code for our routines is shown in below. We used the SciPy and NumPy libraries with CPython and only SciPy with Intel Python. Time measurements were repeated 10 times in a loop, and there was a warm-up calculation prior to each respective benchmark.
We used Python 2.7 with Intel Distribution for Python 2017 Beta and the standard build of Python 2.7.5 in CentOS 7.2. Our system was built on an Intel Xeon Phi processor 7210 with 64 cores clocked at 1.3 GHz, 96 GiB of DDR4 and 16 GiB of MCDRAM memory (high-bandwidth memory, HBM). The HBM was used in flat mode, i.e., exposed to the programmer as addressable memory in a separate NUMA node (see this paper for more information).
# LU decomposition benchmark
import time
from scipy.linalg import \
lu_factor as lu_factor
...
start = time.time()
LU,piv = lu_factor(A, overwrite_a=True, \
check_finite=False)
stop = time.time()# Cholesky decomposition benchmark
from scipy.linalg import \
cholesky as cholesky
...
start = time.time()
L = cholesky(A, overwrite_a=True, \
check_finite=False)
stop = time.time()# SVD benchmark
from scipy.linalg import \
svd as svd
...
start = time.time()
U, s, V = svd(A)
stop = time.time()# DGEMM benchmark
from scipy.linalg.blas import \
dgemm as dgemm
...
start = time.time()
C=dgemm(alpha=1.0, a=A, b=B, c=C, \
overwrite_c=1, trans_b=1)
stop = time.time()Listing 1: Snippets of benchmark code
We did not tune the execution environment of MKL via environment variables. Experiments proved that default choice of the number of threads and thread affinity that MKL makes provides better performance than any alternative settings.
However, to take advantage of the high-bandwidth memory, we placed the entire application in HBM by running the benchmarks with the numactl tool as shown below.
user@knl% numactl -m 1 benchmark-script.pyListing 2: Using numactl to bind the application to HBM.
3. Results and Discussion
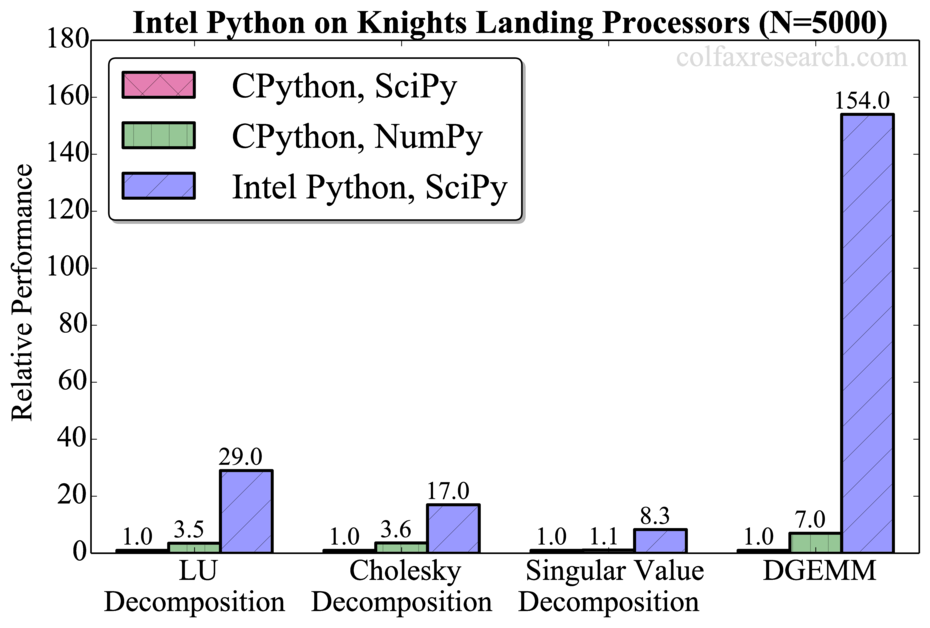
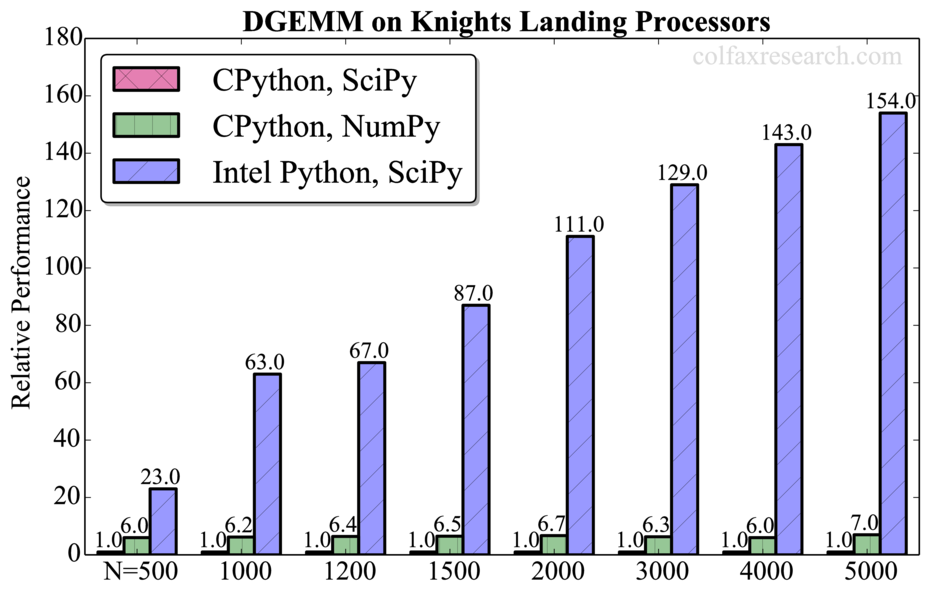
The summary of our benchmarks for matrix size N=5000 is shown in Figure 1. Additional benchmarks are provided in Appendix.
Intel Python showed significant performance gain out-of-the-box with no code tampering.
We have observed that the computation time reported by the Intel MKL library (obtained by setting the environment variable MKL_VERBOSE=1 was lower than the time of the Python call. The difference between them varied from 0.2% to 25% in DGEMM (smaller for larger matrices), from 23% to 60% in LU, from 4% to to 7% in SVD and was over 65% in Cholesky decomposition. We have not investigated the cause of this overhead as our goal was to report out-of-box performance. That said, applications that depend critically on BLAS and LAPACK distribution may benefit from implementation in a compiled language such as C or Fortran.
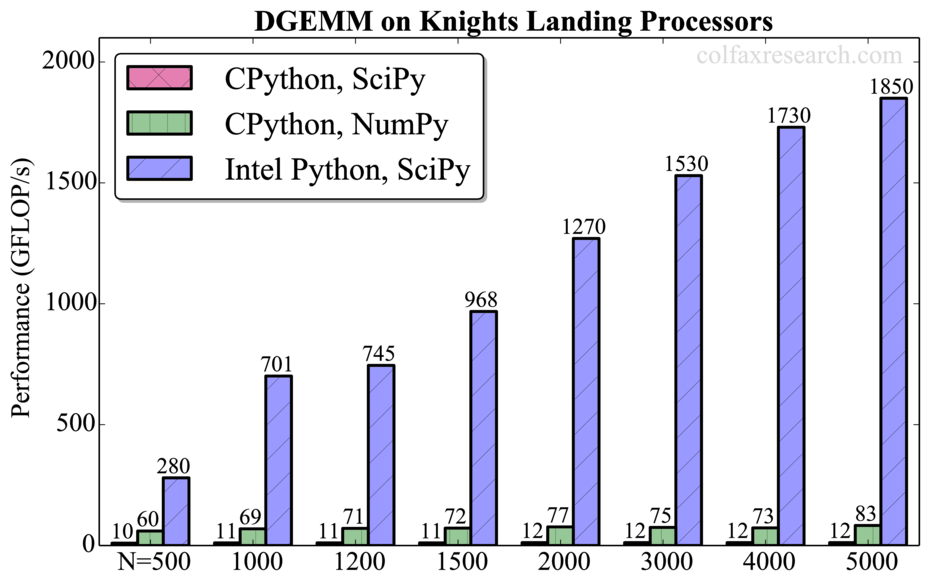
Additionally, we observed that all tested routines are significantly faster in NumPy than in SciPy in CPython (up to a factor of 7 for DGEMM). However, this performance difference is not significant compared to the speedup obtained with Intel Python (up to a factor of 150 for DGEMM). For DGEMM, the attained performance for N=5000 is 1.85 TFLOP/s in double precision (see Appendix), which is 70% of the theoretical peak performance of our processor. Therefore, the usage of Intel MKL remains crucial for extracting the best performance out of Intel architecture.
Performance optimization brought about by Intel Python is not limited to Intel Xeon Phi processors. Intel’s own reports indicate similar high performance gain on general-purpose Intel Xeon processors (see Intel Python page). This is good news for applications that are not highly parallel – either by nature, or due to sub-optimal implementation. High-clock speed cores in Intel Xeon CPUs are better suited for serial workloads than Intel Xeon Phi cores designed for high parallelism.
Intel MKL and Intel distribution for Python are available at no cost (see software.intel.com/en-us/articles/free-mkl). This makes it straightforward to recommend Intel’s software stack over CPython for performance-sensitive computational applications on Intel Xeon Phi processors.
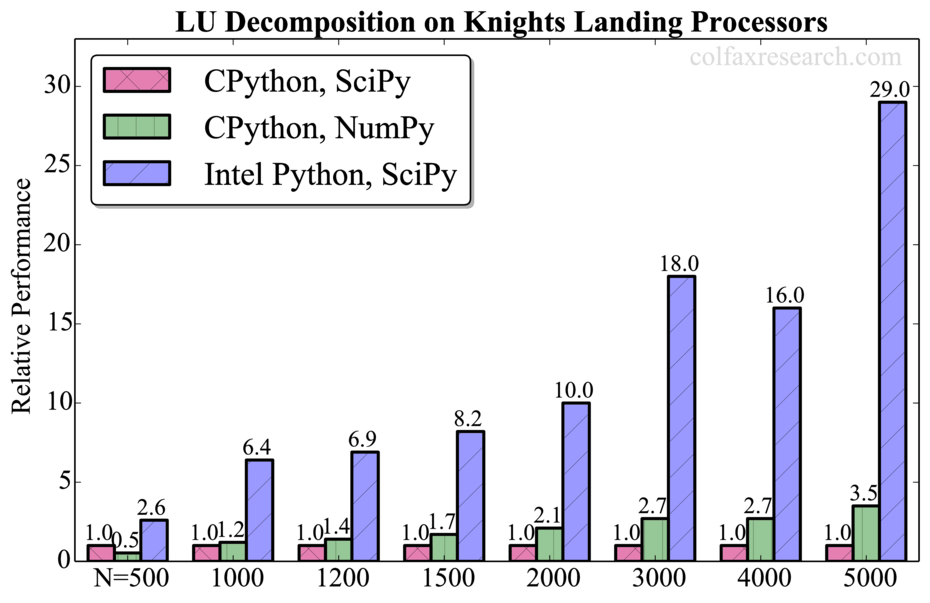
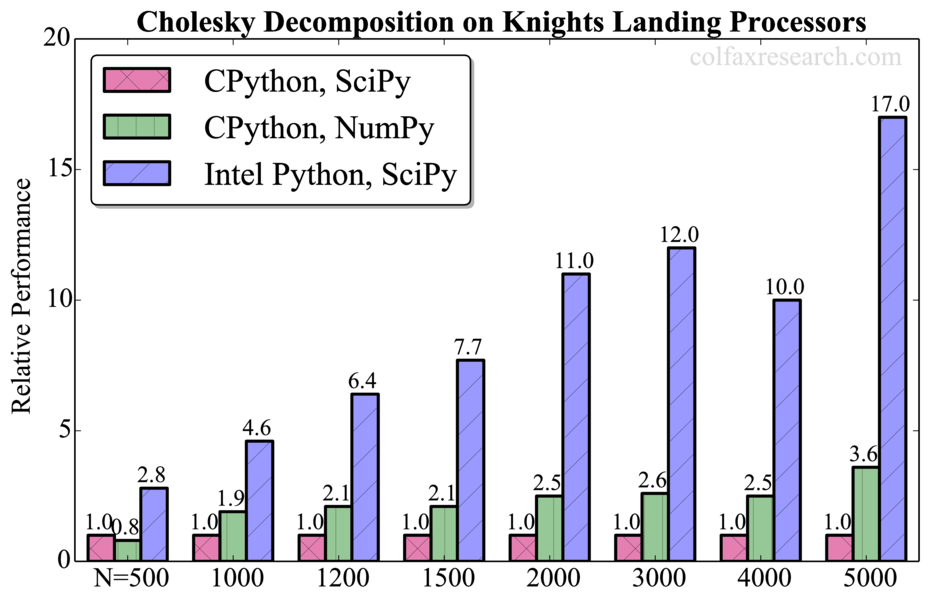
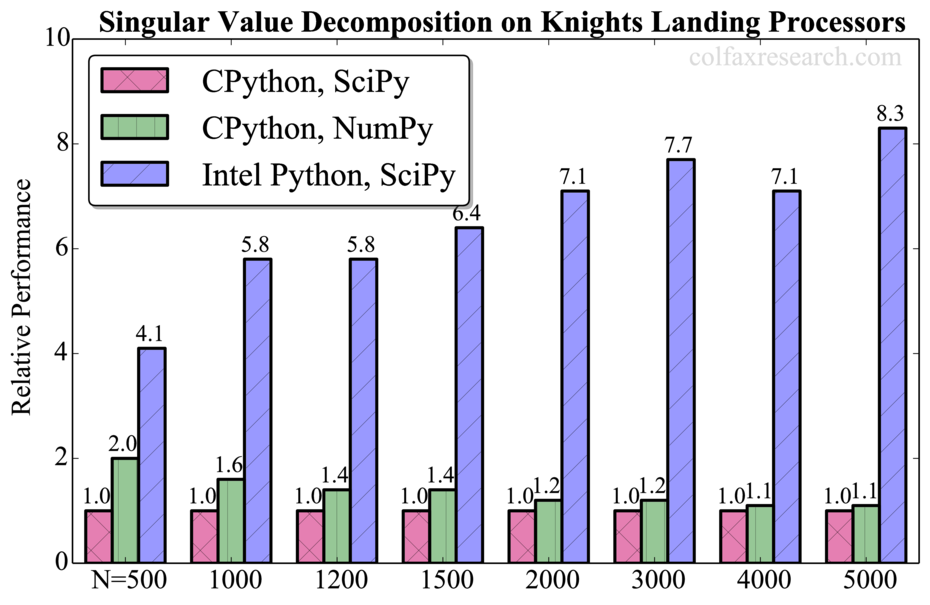
Appendix: Additional Benchmarks
Performance measurements for a range of problem sizes for each of the benchmarked functions are reported below. For DGEMM, we report absolute performance in addition to the relative performance. See remark in Section 3 on the overhead in this function.